实现基本相机模型(针孔)
4.87/5 (18投票s)
实现基本相机模型以扩展光线追踪算法。

引言
扩展我们当前的射线追踪算法,现在我们将实现一个相机类。
目标是能够在任何位置渲染图像,不受限制,因为在我们之前的模型中,观察者必须位于正 z 轴上,即 (0,0,z),z>0。
背景
虽然本文不实现射线追踪,但需要具备高等数学水平,并且阅读 CodeProject 上之前的射线追踪文章。
目标是渲染图像,能够将观察者放置在任何位置,不受限制,而不是像我们之前的模型那样,观察者必须位于正 z 轴上,即 (0,0,z),z > 0。
什么是针孔相机?
“...针孔相机是一种非常简单的相机,没有镜头,只有一个非常小的光圈。简单来说,它是一个不透光的盒子,一侧有一个小孔。来自场景的光线穿过这个单点,并在盒子的另一侧投射出一个倒立的图像。使用小光圈的相机以及人眼在明亮光线下的成像方式都类似于针孔相机。
孔洞越小,图像越清晰,但投射的图像越暗。最佳情况下,光圈的大小应为它与屏幕之间距离的 1/100 或更小……”
参见 http://en.wikipedia.org/wiki/Pinhole_camera
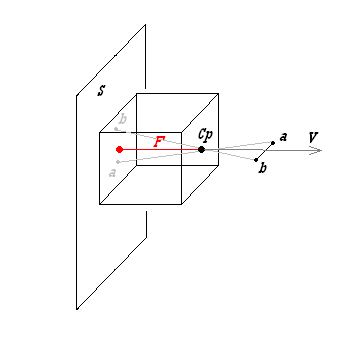
步骤 1 - 定义参数
为了执行所有计算,我们需要一些预定义的参数
- 相机位置 Cp(x,y,z)
- 视角方向向量 V (x,y,z) 归一化……意味着其模长为 1 |V| = 1
- 焦距 F(相机位置 Cp 与相机投影平面 S 之间的距离)
从上述参数,我们可以得到其他有用的参数
- P,平面上的一个点
P = Cp-V*F(x,y,z)
- S 平面方程
根据数学书籍,平面方程的形式为 Ax+By+Cz+D=0
并且如果我们有一个法向量,那么它很简单,幸运的是我们有它,那就是 V。
根据同一本书……
A = Vx
B = Vy
C = VZ我们需要得到 D,但现在很简单,因为我们有一个平面上的点
所以 D = -(A*Px+B*PY+C*PZ)
A = normalVector.x;
B = normalVector.y;
C = normalVector.z;
D = -(normalVector.x * point.x + normalVector.y * point.y + normalVector.z * point.z);
相机坐标系
现在我们称针孔模型为相机坐标系。
所以为了表示一个模型,我们现在有一个笛卡尔坐标系 x,y,z 以及一个相机坐标系。
我们的计划是将相机坐标系平移和旋转,以适应参考笛卡尔坐标系,为此我们需要一些关于球面坐标的方程来获取 theta 和 phi 角。
“...在数学中,球面坐标系是一种三维空间坐标系,其中一个点的位置由三个数字指定:该点与固定原点的径向距离,从固定平面测量的其仰角,以及在同一平面上测量的其正交投影的方位角,从固定参考方向测量。仰角通常被倾斜角取代,该倾斜角从垂直于参考平面的天顶方向测量……”
参见 http://en.wikipedia.org/wiki/Spherical_coordinate_system

根据我的数学书,我们知道了如何将给定的 R3 点表示为球面坐标以及转换……(稍后将使用)。
笛卡尔坐标转换为球面坐标
x = R sin (phi) cos (theta)
y = R sin (phi) sin (theta)
z = R cos (phi)
球面坐标转换为笛卡尔坐标
R = sqrt(x2+y2+z2)
S = sqrt(x2+y2)
phi = acos(z/R)
theta = x>=0 asin(y/S)
x<0 PI - asin(y/S)
下面是如何计算 phi 和 theta 角,这将帮助我们旋转坐标系以适应参考系统
Point oNormalizedDirection = Algebra.Normalize(m_oDirection.x,
m_oDirection.y, m_oDirection.z);
// calculate frontpoint
m_oFrontPoint = new Point(m_oOrigin.x + oNormalizedDirection.x,
m_oOrigin.y + oNormalizedDirection.y,
m_oOrigin.z + oNormalizedDirection.z);
// 1 translate to origin
Point oTranslatedFrontPoint = new Point(m_oFrontPoint.x - m_oOrigin.x,
m_oFrontPoint.y - m_oOrigin.y,
m_oFrontPoint.z - m_oOrigin.z);
// calc phi & theta
double x2 = oTranslatedFrontPoint.x * oTranslatedFrontPoint.x;
double y2 = oTranslatedFrontPoint.y * oTranslatedFrontPoint.y;
double radius = Math.Sqrt(x2 + y2 + oTranslatedFrontPoint.z * oTranslatedFrontPoint.z);
double s = Math.Sqrt(x2 + y2);
m_dPhi = Math.Acos(oTranslatedFrontPoint.z / radius);
m_dTheta = 0;
if (Math.Abs(s) > 1.0E-5)
{
if (oTranslatedFrontPoint.x >= 0)
{
m_dTheta = Math.Asin(oTranslatedFrontPoint.y / s);
}
else
{
m_dTheta = Math.PI - Math.Asin(oTranslatedFrontPoint.y / s);
}
}
计算投影

Projection
我们的第一个目标是计算在平面 S 上的投影点 a。
如何获得这个?
再次从我旧的数学书……
如果我们知道直线和平面方程,我们可以很容易地计算出它们的交点,并且再次幸运的是我们知道!
我们的直线方程的参数形式是 r = p + t*v。
- p 是直线上的任意一点,t 是一个标量
- v 是直线向量
- 我们的 p 是点 a
- 我们的 v 可以从相机位置到 a 计算得出,即 Cp-a
使用这个参数方程相对于平面方程,我们找到参数 t,从而通过以下方式找到交点
- t 值在 p + tv
代码
public Point GetIntersection(Point p, Point Origin)
{
Vector v = new Vector(p, Origin);
double E = (v.x * A + v.y * B + v.z * C);
if (Math.Abs(E)<1.0E-5)
{
return null;
}
v = Algebra.Normalize(v.x, v.y, v.z);
double t = -(A * p.x + B * p.y + C * p.z + D) / (E);
return new Point(p.x + t * v.x, p.y + t * v.y, p.z + t * v.z);
}
我们的最终目标是将这个交点映射到我们的屏幕上。
为此,我们需要使用计算出的 phi 和 theta 将点拟合到我们的参考坐标系中……
代码
public Point LocalToCartesian(Point point)
{
point.x -= m_oOrigin.x;
point.y -= m_oOrigin.y;
point.z -= m_oOrigin.z;
rtPoint.RotZ(-m_dTheta, ref point.x, ref point.y);
rtPoint.RotY(m_dPhi, ref point.x, ref point.z);
return new Point(point.x, point.y, point.z);
}
Using the Code
所有需要的代码都在文章顶部的 zip 文件中的一个项目中,只需下载并编译。
关注点
独自一人,并且仅使用数学而不是库来改进算法是非常有挑战性的。许多人问我为什么要做一些已经存在于许多库中的东西。我的回答是我喜欢挑战、发现,看到自己通过双手和努力取得的成果是非常令人满意的。
历史
创建相机类是射线追踪文章系列的下一步,它将带我们进入下一个阶段,并使我们能够开始创建动画。
