使用调用堆栈解析数学方程式
4.96/5 (16投票s)
使用调用堆栈而不是正则表达式来解构数学公式并计算值。
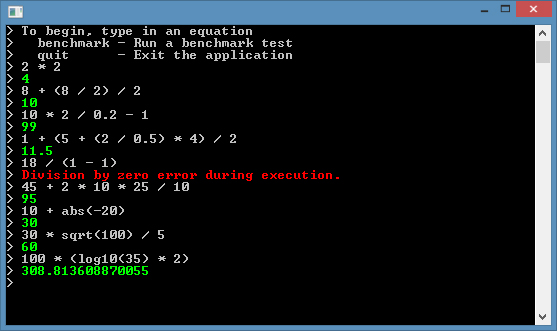
引言
本文的目的是开发和探索一个实用程序,用于获取基于文本的数学算法并对其进行解析以生成实际的数值。此外,该实用程序还应具有可扩展性,以便开发人员能够提供自定义方法和扩展来对值执行进一步的操作。本文还讨论了使用基于文本的解析器和基于标记或调用堆栈的解析器之间的区别。
背景
开发这个框架的想法是在阅读了几篇关于解析算法的文章后产生的。普遍的趋势似乎是使用正则表达式 (Regex) 来提取数学公式集并执行它们,最终得到一个最终值。
相反,本文将重点构建一个“指令堆栈”,该堆栈将按优先级顺序执行以计算最终值。堆栈将通过解析数学公式的单个字符,然后确定堆栈的类型、顺序和层级,然后执行以生成结果值来生成。
正则表达式 vs. 调用堆栈
正则表达式
在解析公式时使用正则表达式的理论是,该库能够根据匹配条件动态替换文本,这通过首先提取最高优先级运算符来简化执行顺序的过程。例如
function execute(string formula)
{
for each brackets in formula:
replace brackets in formula = execute (brackets)
for each division in formula
replace division in formula = division.left / division.right
for each multiply in formula
replace multiply in formula = multiply.left * multiply.right
for each subtract in formula
replace subtract in formula = subtract.left - subtract.right
for each addition in formula
replace addition in formula = addition.left + addition.right
return (formula as double);
}
这段粗略的伪代码只是表示使用正则表达式的代码将如何迭代字符串公式。凭借正则表达式在字符串中替换内联文本的能力,每次迭代公式都会用运算符的结果替换数学运算符。
因此,使用上面的伪代码,让我们考虑以下公式
2 + 5 * 10 / 2 + (100 - 90)
首先,`execute()` 方法将匹配 `(100 - 90)` 满足函数的括号条件,从而在括号内的内部公式上调用相同的 `execute()` 方法,并执行 `100 - 90` 并从内部调用返回结果。在正则表达式替换字符串中的括号后,公式将变为
2 + 5 * 10 / 2 + 10
该方法将继续搜索除法运算符,它将匹配字符串中的 `10 / 2`,使用运算符左右的值执行除法,并替换字符串中的值,导致公式看起来像这样
2 + 5 * 5 + 10
该方法将继续识别乘法(`5 * 5`)并将其替换为字符串中操作的结果值,然后未能识别减法运算符,这使我们得到以下操作
2 + 25 + 10
在此阶段,该方法将处理每个加法运算符(`2 + 25`,然后是`27 + 10`),替换字符串中的值,最终将在字符串中留下值`37`。最后,该方法将数字转换为 C# `double` 类型并从方法中返回值。
使用正则表达式进行此操作是可取的,因为它使处理数学公式成为一个简单的过程。字符串操作易于执行,并且正则表达式识别匹配序列和字符组并能够用值替换它们的能力减少了所需的手动工作量。此外,数学函数和变量的实现非常容易满足,因为正则表达式可以根据字符的精确序列匹配条件。
调用堆栈
创建数学序列的“调用堆栈”思想是为了避免在处理字符串公式时使用正则表达式。相反,公式被分解成信息块,这些信息块被识别为操作,并按重要性顺序执行。如果一个块是子堆栈(例如公式中括号内的任何部分,需要在过程使用值之前作为子公式执行[很像前面提到的正则表达式方法]),那么这些可以作为需要调用的可调用块进行嵌套。
本文中实现“调用堆栈”的方法是使用灵活的结构,这些结构可以充当三种不同类型之一:数值、子块(需要解析的公式)或方法调用。为了保留此信息,单个结构必须能够存储任何数据,结构如下
struct block
{
byte[] operations;
block[] stack;
block_method method;
double value;
};
在上述 C# 库中使用的结构精简版中,该结构可以使用以下逻辑充当三种不同类型。
重要的是要知道,结构的 `value` 字段将始终包含块的值:如果块是可执行的(例如嵌套块或公式,或方法调用),则 `value` 字段将在执行后包含执行结果。
数值
当块只是一个数值时,块的 `value` 字段将填充该数字。
公式
当在公式中检测到子公式(例如括号之间的任何内容)时,该块将构造为另一个公式。 `value` 字段默认包含零值,直到该块被执行。
方法调用
当在公式中检测到方法调用时,`block_method` 字段会填充,其中包含方法的名称和逗号分隔的参数列表。 `value` 字段默认包含零值,直到方法调用被执行。
那么,这对执行顺序意味着什么?这些是如何结合在一起的,以及块究竟是如何处理的?
我们来考虑下面的公式
2 + 2 * 3
这是一个相对简单的操作,但需要将其转换为操作堆栈。因此,我们按顺序(从左到右)遍历公式。
解析为调用堆栈
解析算法做的第一件事是分配一个“父块”,它是 `block` 结构的一个实例,它将作为公式的最高所有者。完成此操作后,`operations` 字段将被初始化为一个新的字节数组,并且 `stack` 字段将被构造。解析器将然后遍历公式以识别字段。
解析器将在公式开头找到数字 `2`。这是一个简单的数字,并将以此方式保留在块中。将为该数字分配一个新的 `block` 结构,并且 `value` 字段将填充数字 `2`。解析器将然后将此新块追加到父块的 `stack` 数组中,索引为 `0`,然后将该块的索引记录在 `operations` 字段中作为第一个字节。
在此阶段,父块的结构如下
stack[0] = block { .value = 2 };
operations = {
00
};
解析器将识别的下一个项是加法运算符。运算符不需要新的块结构,因为它不代表一个值。操作数组遵循特定的顺序,其中每个奇数索引代表一个运算符(因此索引 1, 3, 5 等处的任何字节将始终是前一个块和下一个块之间的运算符)。
解析器将在下一个索引处将代表加法运算符的字节(在此项目中为 0x03)附加到操作数组中,因此父块将如下所示
stack[0] = block { .value = 2 };
operations = {
00, 03
};
按照相同的操作序列,解析器将识别另一个代表数字 2 的块,并将其附加到堆栈中。接下来,运算符 * 代表乘法运算符,并将其直接附加到操作数组中(代表乘法的字节为 0x05)。最后,数字 3 将被解析并作为新块附加,并在操作数组中注册。
完成这些操作后,父块将如下所示
stack[0] = block { .value = 2 };
stack[1] = block { .value = 2 };
stack[2] = block { .value = 3 };
operations = {
00, 03, 01, 05, 02
};
简单来说,00、01 和 02 字节代表堆栈中块的索引,而 03 和 05 分别代表加法和乘法运算符。
执行调用堆栈
调用堆栈的执行相对简单。为了计算公式的正确值,我们必须首先执行所有优先级最高的运算符。这可以通过遍历父块的 `operations` 字段,检查每个奇数索引(`1`、`3`、`5` 等)并交叉检查运算符来实现。
function execute(block parent)
{
order = { 05, 03 }
operations = parent.operations
for each operator in order
{
for i = 1; operations.Length > i; i = i + 2
{
if operations[i] == operator then
calculate(operations, i)
}
}
}
如上述伪代码所示,我们遍历并检查每个运算符。`order` 变量存储运算符必须执行的顺序。如果匹配到运算符,我们将在操作数组上使用当前数组中的索引执行一个尚未定义的 `calculate()` 函数。
此公式中 `calculate()` 函数的目的是对运算符索引左右的值执行运算符。为此,请考虑以下函数
function calculate(block[] operations, int index)
{
double left = operations[index - 1].value
double right = operations[index + 1].value
byte operator = operations[index];
switch operator
{
when add: left += right; break;
when sub: left -= right; break;
when mul: left *= right; break;
when div: left /= right; break;
}
operations[index - 1].value = left;
operations[index + 1].value = left;
}上述伪代码有一个简单的目的,即消耗运算符周围块的左右值,然后对这些块执行运算符命令。代码然后用计算出的左值更新这两个块,以便如果对任一块执行单独的运算符,它们都包含最新值。
实际上,这个函数的实现要复杂一些。本文提供的示例有一个更新“链式”链接块的过程。例如,以下面的公式为例
2 + 5 * 5 * 5 - 1
如果使用上述查询执行此操作,则值将无法正确计算,因为块不会水平同步。运行顺序将如下所示
2 + 25 * 25 * 5 - 1 2 + 25 * 125 * 125 - 1 2 + 25 * 125 * 124 - 124 27 + 27 * 125 * 124 - 124
这可能看起来令人困惑,但请考虑值始终分配给左侧。如果只处理一个链接,则此公式的最终结果值可能为 `27`,因为我们尚未将对其他值所做的更改拖过来。如果您查看我们示例应用程序的 `MQ.cs` 文件中的 `Execute()` 方法,您会看到更改已应用于任何先前计算过的值。
请参阅下面的代码,其中任何以**粗体**突出显示的值都已修改,并应成为未来更新的目标
2 + 25 * 25 * 5 - 1 2 + 125 * 125 * 125 - 1 2 + 124 * 124 * 124 - 124 126 + 126 * 126 * 126 - 126
以上代码现在产生结果 126,这实际上是我们需要的值。这可能看起来令人困惑,但应该理解的是,任何已计算过其值(粗体显示)的值都不会再次计算,但当任何直接链接到左侧或右侧的块的值发生更改时,它将被更新。公式中操作的最新值始终存储在左侧,这意味着它应该可以通过操作顺序访问。
为了更好地理解此过程,下图突出显示了计算的每个阶段,其中橙色突出显示的块是接下来要计算的块,绿色突出显示的块表示以前已计算过的块。直接位于任何其他橙色或绿色块旁边的绿色(或橙色)块将受到计算结果的影响

每当一个运算符完成时,左右节点就会链接起来。随着运算符相邻执行,这种链接会继续传播,从而导致操作的值在节点链接的公式中共享。
换一种方法,考虑下面的公式,它有两个高优先级运算符,由较低优先级的加法和减法运算符分隔开来
2 * 2 + 1 - 20 / 2
将首先运行的两个运算符分别是除法(20 / 2)和乘法(2 * 2)。这意味着这两个块不会连接,因为一个 1 的加法介于这两个块之间。这会产生以下操作顺序
2 * 2 + 1 - 10 / 10 4 * 4 + 1 - 10 / 10
在此阶段,`1` 是公式中唯一未计算的块,这意味着它成为下一个首先执行的运算符的主题。在这种情况下,这是减法运算符,然后是加法运算符
4 * 4 + -9 - -9 / -9 -5 * -5 + -5 - -5 / -5
`1 - 10` 操作的值发生,将代表 `1` 的块的值更新为 `-9`,但值 `-9` 未传递到 `4 * 4` 块,因为加法运算符尚未执行,并且未链接到公式的右侧。只有当加法运算符执行后,左侧才会被更新,其值为 `4 + -9`
用与前面类似的图表可视化,它将是这样的

这类似于链表,其中节点使用引用节点位置的 `left` 和 `right` 字段连接。每当在公式中首次创建块时,`left` 和 `right` 字段都不引用其他块。但是,一旦执行了块,`left` 字段的值指向 `right` 字段的值,反之亦然。
如果执行另一个块,并且 `left` 或 `right` 字段有一个链接到另一个块的值,则更新任一字段中的块,并且相同的迭代继续发生,直到 `left` 或 `right` 字段不再有引用。
执行括号
括号操作作为其自己的块存储在父块的 `stack` 字段中。它们以这种方式存储,因为它们代表一个需要执行才能产生值的子公式,然后该值可以在父公式中正常使用。
考虑下面的公式,它将括号用作其中一个操作
2 * (2 + 2)
如果使用上述执行方法,解析器将在添加额外的 `2` 之前执行 `2 * 2`。相反,为了将 `2 + 2` 分离为可执行的子公式,公式中的值应包含在一个可执行块中。
因此,在为此操作构建调用堆栈时,解析顺序将从将 2 和乘法符号解析到父块开始
stack[0] = block { .value = 2 };
operations = {
00, 05
};此时,解析器将识别到已匹配到一个开括号,这表示子公式的开始。将构造一个新块以准备将其附加到堆栈中,但不是设置新块的 `value` 字段,而是从开括号后的索引处调用相同的解析函数,并将此新块作为调用堆栈的目标。
解析器将识别并存储新块中括号内的值
child_stack[0] = block { .value = 2 };
child_stack[1] = block { .value = 2 };
child_operations = {
00, 03, 01
};一旦达到闭括号,嵌套解析函数将退出,父块现在有一个子块,该子块分配有一组 `operations` 和一个 `stack`,值为零。父块现在将此子块附加到 `operations` 数组中并继续向前。父块最终将如下所示
stack[0] = block { .value = 2 };
stack[1] = block
{
stack[0] = block { .value = 2 };
stack[1] = block { .value = 2 };
operations = {
00, 03, 01
};
};
operations = {
00, 05, 01
};在此阶段,该块已准备好执行。这次唯一的区别是堆栈中的第二个块需要在 `value` 字段使用之前执行。
为此,我们需要对我们之前创建的 `calculate()` 伪函数进行一些小的修改,以确保该块被执行
function calculate(block[] operations, int index)
{
if operations[index - 1].stack is not null then
execute(operations[index - 1]);
if operations[index + 1].stack is not null then
execute(operations[index + 1]);
double left = operations[index - 1].value
double right = operations[index + 1].value
byte operator = operations[index];
switch operator
{
when add: left += right; break;
when sub: left -= right; break;
when mul: left *= right; break;
when div: left /= right; break;
}
operations[index - 1].value = left;
operations[index + 1].value = left;
} 所添加的只是一个检查,用于查看操作块是否包含自己的堆栈,这意味着在将 `value` 字段用于计算之前,需要对该块执行一个操作。当对该块调用执行函数时,`stack` 和 `operations` 字段将设置为 `null`,以便将来对该块的引用使用计算值或公式分配的最新值。
执行方法
实现对自定义方法的支持以非常相似的方式工作。在解析例程期间,如果解析器遇到任何函数名称字符(a-z、A-Z 或下划线),它将开始一个“函数”循环。这基本上通知解析器它需要准备构建一个表示方法调用的堆栈块
10 + pow2(2)
使用上述公式,解析器将标准地识别 `10` 和加法运算符,并将这些值附加到 `stack` 和 `operations` 字段中。
此时,下一个识别的字符是 `p`,因此解析器进入“解析方法”状态,该状态读取所有有效字符(a-z、A-Z、0-9 或下划线),直到遇到括号或空格。一旦遇到开括号,解析器进入“解析方法参数”状态,该状态从开括号后的索引处调用脚本上的相同解析方法。请参阅下面的解析结构,其中引号内的每个部分都是当前解析目标
'pow2'(2)
The name of the method is extracted ('pow2')
pow2'('2)
The opening bracket is matched, and the parser begins the parameter parsing mode.
pow2('2')
The digit 2 is extracted from the parameters.
pow2(2')'
The closing bracket is matched, the script leaves the method parsing states.要更深入地了解确切的过程,请参阅 `MQ.cs` 文件中的 `ParseMethod` 方法。
最后,一旦方法名称和参数成功地从公式中解析出来,解析器就会构建一个 `block_method` 对象,并复制方法名称和参数。然后将此 `block_method` 存储在一个新的 `block` 对象的 `method` 字段中,并将其推入堆栈(与任何数字或子公式块相同)。
因此,对于上面描述的公式,堆栈将如下所示
stack[0] = block { .value = 10 };
stack[1] = block
{
method = block_method
{
parameters[0] = block { .value = 2 };
name = "pow2";
};
};
operations = {
00, 03, 01
};堆栈索引 `1` 处的块默认值为零。`calculate()` 方法需要进行类似更改,以确保在 `value` 字段使用之前调用该方法
function calculate(block[] operations, int index)
{
if operations[index - 1].method is not null then
invoke_method(operations[index - 1])
if operations[index + 1].method is not null then
invoke_method(operations[index + 1])
if operations[index - 1].stack is not null then
execute(operations[index - 1])
if operations[index + 1].stack is not null then
execute(operations[index + 1])
double left = operations[index - 1].value
double right = operations[index + 1].value
byte operator = operations[index]
switch operator
{
when add: left += right
when sub: left -= right
when mul: left *= right
when div: left /= right
}
operations[index - 1].value = left
operations[index + 1].value = left
} 添加了一个检查以验证左右堆栈块的 `method` 字段是否已分配。如果是这种情况,则对相关块调用 `invoke_method()` 函数以计算值。
下面是上面公式中 pow2 方法如何实现的示例
function invoke_method(block parent)
{
for i = 0; parent.parameters.Length > i; i = i + 1
{
execute(parent.parameters[i])
}
if parent.method.name = "pow2" then
parent.value = parent.parameters[0].value ^ 2;
parent.method = null
} 该方法对每个参数执行操作(以防这些参数也是方法调用或子公式),然后检查方法的名称以执行 pow2 函数。一旦成功调用该方法,块的 `value` 字段将被赋值,并且 `method` 字段将重置为 `null` 以防止再次调用。
Using the Code
入门
随附的示例项目包括一个类库项目 (MQ) 和一个控制台应用程序项目 (MQExample),您可以用于测试。
要开始使用解析器,请构造并存储 `MQ` 类的新实例。建议保留该类的持久副本,而不是动态创建实例。
private System.Parsers.MQ parser = new System.Parsers.MQ(); 执行数学公式就像调用类的 `Calculate()` 方法一样简单。该方法接受一个字符串参数,该参数是公式的文本表示,用于计算。例如
public double GetFormulaValue()
{
return parser.Calculate("2 * 5 / 3 + (1 * 2 * 3) / (4 - 2)");
}添加函数
解析器还支持注册自定义函数。任何可以由解析引擎处理的函数都必须实现 `MQFunctionHandler` 签名,如下所示
double MQFunctionHandler(MQParameters e);
该函数必须返回一个 `double` 值,作为方法调用的结果。`MQParameters` 类是传递给方法的所有参数的集合。参数中的每个值都是一个 `double` 值。
myFunction(1, (2 * 3), ((1 + 1) / 0.25))
这将生成一个带有以下值的 `MQParameters` 列表
e[0] = 1.00 e[1] = 6.00 e[2] = 8.00
要为“myFunction”注册函数处理程序,我们只需创建一个 `MQFunction` 对象的新实例,并将其附加到解析器的 `Functions` 属性中。`MQFunction` 对象的构造函数接受多个参数,这些参数决定了函数的行为
MQFunction(string name, MQFunctionHandler callback);MQFunction(string name, MQFunctionHandler callback, int parameters);MQFunction(string name, MQFunctionHandler callback, int minParams, int maxParams);
name- 在公式中识别的方法名称。callback- 当在公式中调用方法时将引发的回调方法。parameters- 方法所需的精确参数数量。minParams- 方法所需的最小参数数量。maxParams- 方法将接受的最大参数数量。
要注册“myFunction”方法的实例,我们添加函数如下
private void SetupFunctions()
{
parser.Functions.Add(new MQFunction("myFunction", new MQFunctionHandler(MyFunction), 3));
}
private double MyFunction(MQParameters parameters)
{
return parameters[0] + parameters[1] + parameters[2];
} 或者,使用匿名函数和 lambda 表达式
parser.Functions.Add(new MQFunction("myFunction", (e) => { return e[0] + e[1] + e[2]; }, 3)); 因此,任何对“myFunction”方法的调用都将三个参数相加并返回结果,然后将其放入方法调用的调用堆栈中。
注意
MQ 类自带一些基本的数学函数。这些函数包括 `abs(x)`、`ceil(x)`、`cos(x)`、`floor(x)`、`log(x, y)`、`log10(x)`、`max(x, y)`、`min(x, y)`、`pow2(x)`、`round(x)`、`round(x, y)`、`sin(x)`、`sqrt(x)` 和 `tan(x)`
基准测试
对 MQ 解析器进行了比较基准测试,其中包括三个替代解析库
- Math Parser .NET
https://codeproject.org.cn/Articles/274093/Math-Parser-NET
此库使用正则表达式来提取公式和函数以供执行。 - Math Processor
https://codeproject.org.cn/Articles/500327/Building-a-General-Purpose-Interpreter-Math-Engine
此库使用基于令牌的方法从表达式中提取运算符和值,并按顺序执行它们。 - Calculation Engine for .NET
https://codeproject.org.cn/Articles/246374/A-Calculation-Engine-for-NET
此库也使用基于令牌的方法来解析表达式,类似于 Math Processor 库。
基准测试结果如下
MQ - MQ Parser MPN - Math Parser .NET MP - Math Processor CE - Calculation Engine for .NET Formula | Cycles | MQ (ms) | MPN (ms) | MP (ms) | CE (ms) ----------------------------------------------------------------------- E1 | 100 | 11.008 | 91.0592 | 50.0352 | 1.9968 E1 | 1000 | 4.0064 | 309.2096 | 33.0112 | 2.0096 E1 | 10000 | 40.0256 | 3015.0144 | 337.2288 | 124.0832 ----------------------------------------------------------------------- E2 | 100 | 0.9984 | 35.0336 | 4.992 | 0.00 E2 | 1000 | 5.9904 | 330.2144 | 46.0416 | 2.9952 E2 | 10000 | 59.0464 | 3268.1856 | 458.304 | 449.3056 ----------------------------------------------------------------------- E3 | 100 | 7.0016 | 66.048 | 19.008 | 0.9984 E3 | 1000 | 8.9984 | 612.416 | 57.0368 | 3.9936 E3 | 10000 | 84.0448 | 6127.104 | 577.3824 | 575.3856 ----------------------------------------------------------------------- E4 | 100 | 0.9984 | 36.032 | 7.0016 | 0.00 E4 | 1000 | 9.0112 | 359.232 | 63.04 | 4.0064 E4 | 10000 | 81.0496 | 3585.3952 | 630.4256 | 573.376 ----------------------------------------------------------------------- E5 | 100 | 3.008 | 120.0768 | 6.0032 | 1.0112 E5 | 1000 | 14.0032 | 1180.80 | 57.0368 | 4.992 E5 | 10000 | 131.0848 | 11799.8976 | 565.376 | 460.3008 ----------------------------------------------------------------------- E6 | 100 | 2.9952 | 51.0336 | 10.0096 | 0.9984 E6 | 1000 | 18.0096 | 479.3216 | 101.0688 | 8.00 E6 | 10000 | 163.1104 | 4821.2224 | 1013.6704 | 361.2416 -----------------------------------------------------------------------
这些是执行不同方程后,基准测试(在随附的源代码中可用)的单次执行结果。每个公式的方程如下,其中字母 R 表示为公式的每个循环生成的随机值
E1 - 100.00 * 50.00 + (R / 123.00) E2 - 20.00 / (3.35 * 0.52) / (R / 2.05) * 4.32 E3 - 4.00 * 2.00 / 0.345 * R / 7.42 * cos(8.83) / 0.128 E4 - 1.00 + (200.00 * (2.00 * 100.00 / 8.00) / (8.00 + 10.00)) * R E5 - cos(tan(R) * 0.293) / sin(2.3994 * R) E6 - ((2.12 / 1200) * ((1 + 2 / 1200) * (1 + 2 / 1200)) / ((1 + 2 / 1200) * (1 + 2 / 1200) - 1)) * R
基准测试突出显示,MQ 解析器引擎的功能显着快于 Math Parser .NET 库(使用正则表达式方法)和 Math Processor 库(使用令牌)。
然而,MQ 解析器引擎在公式循环次数较少时,性能低于 Calculation Engine 库。相比之下,在公式循环次数较多时,MQ 解析器引擎的性能更优。对此的一种潜在解释可能是,MQ 解析器不使用任何集合来存储数据块。相反,MQ 解析器在表达式执行之前分配一个固定大小的数组,并且只在达到限制时才扩展。虽然 `ArrayList` 对象可以执行相同的功能,但使用集合对象意味着分配对象周围的所有内存,并完全依赖该对象尽可能高效地执行,这由于需要将 `ArrayList` 的项转换回原始类型而略受阻碍。
无论如何,基准测试突出了一个事实:使用正则表达式解析公式效率非常低。即使正则表达式经过预编译并在字符串上执行,处理字符串中的符号、执行相应的计算,然后替换原始字符串中的值,也是一个漫长而昂贵的过程。提取符号并分配少量内存来存储信息要有效得多,因为这个过程本质上与将数据从一个位置(字符串)移动到另一个位置(目标块)并运行此内存通过执行算法相同。
摘要
尽管使用正则表达式使解析计算变得更容易,减少了开发人员所需的工作量,但这并不是在表达式密集型软件中使用的最佳方法。正则表达式是一个昂贵的实用程序,尤其是在表达式变得更大更复杂时,增加了对字符串的搜索次数和替换次数。
在解析表达式时使用标记化或调用堆栈方法可能构建起来很繁琐,但性能提升值得额外的开发时间。如果我们将相同的原则应用于“伪代码”解析器,该解析器解剖和解释自定义脚本语言,那么使用正则表达式解析器将变得不切实际。
一旦我们发现子表达式和函数可以转换为它们自己的块,管理这些表达式就变得更容易。开发解析器时遇到的更困难的问题之一是如何在处理数学时考虑优先级顺序。特别是在伪代码解析器中,一旦开发人员开始线性思考,设计能够有效处理嵌套代码的代码就成为一个问题。相反,嵌入节点和块是解决这些优先级和嵌套问题的一些实用方法。
关注点
我明白本文中用于基准测试的一些项目相当陈旧。本文的目的是更多地强调使用调用堆栈的效率,而不是实际开发一个以最高速度和准确性运行的库。本文可能更多地被用作参考,供那些对生成自己的脚本和表达式树解析器感兴趣的人使用,而不是作为实际的表达式解析库。
MQ 解析器在解析表达式时遗漏了一些基本概念。源代码中未解决的一些基本数学问题包括
- 数字的正负前缀不能正常工作。例如
2 - -2
这将无法正常工作,因为 MQ 解析器期望在运算符后面跟一个数字。这可以在源代码中轻松修复,但我没有时间解决这个问题。 - 缺少许多附加/理想的运算符,例如:
<< >> | & ~
历史
- 1.0.0 - 2014 年 4 月 3 日 - 初稿。
- 1.0.1 - 2014 年 4 月 7 日 - 重新上传 ZIP 存档以包含所有解决方案文件。
