Spirograph 形状:数学公式生成的 WPF 贝塞尔形状
4.99/5 (136投票s)
一组形状:外摆线、外差向曲线、内摆线、内摆线、菲里斯轮、李萨如图形和玫瑰曲线。

引言
本文介绍了一组您可以在应用程序中使用的形状。其中一些,例如外差向曲线和外摆线,如果您小时候玩过 Spirograph,可能会很熟悉。这里包含的所有形状都由简单的数学关系定义。菲里斯轮是唯一一个稍微复杂一些的。然而,直到最近,将数学定义的函数转换为矢量图形一直相当费力。改变源于我的上一篇文章(GraphDisplay:用于绘制函数和曲线的基于贝塞尔的控件),在该文章中,我开发了一种生成表示数学定义的曲线和函数的 PathGeometry 元素的程序。此类代码的一种用途是制作实用的业务或科学应用程序。另一种用途(此处选择的用途)是能够毫不费力地在应用程序中包含一些令人愉悦的数学矢量形状。特别地,完全不需要理解所有这些背后的数学知识就可以在您的应用程序中使用这些形状。只有在创建您自己的其他形状时才需要一些数学知识,但即使那时,理解所有这些背后的算法也是完全可选的。
背景
关于形状的内部工作原理和形状本身,有很多有趣的背景知识。如果您想了解应用程序的工作原理,请参阅我的文章 GraphDisplay:用于绘制函数和曲线的基于贝塞尔的控件。对于这些形状,以下参考资料可能有所帮助
- 内摆线 - 维基百科内摆线,MathWorld 内摆线
- 内差向曲线 - 维基百科内差向曲线,MathWorld 内差向曲线
- 外摆线 - 维基百科外摆线,MathWorld 外摆线
- 外差向曲线 - 维基百科外差向曲线,MathWorld 外差向曲线
- 玫瑰 - 维基百科玫瑰曲线,Mathworld 玫瑰曲线
- 李萨如图形 - 维基百科李萨如图形,MathWorld 李萨如图形
- 菲里斯轮 - Mathematica 演示:菲里斯轮,Mathematica 演示:轮子上的轮子上的轮子
Mathematics Magazine 上还有一篇 F. A. Farris 的文章,“Wheels on Wheels on Wheels - Surprising Symmetry”,Mathematics Magazine 69(3),1996 年 pp. 185-189。遗憾的是,这篇文章在线上(至少免费)不可用,但几乎可以在任何大学图书馆中轻松找到。
如何使用
这些形状可以像任何其他形状一样使用。
<f:Rose A="40" N="3" D="2" Stroke="Gray" Fill="DarkSlateGray"/>
创建一个 Rose,非常类似于上面图片中的那个。您需要添加 f 的 XML 命名空间。
xmlns:f="clr-namespace:FunctionalShapes;assembly=FunctionalShapes"
真的没有太多要说的了。问题在于您可能不知道如何通过参数控制形状的外观。为此,演示应用程序是内在形状的各种可能性的演示。
这些形状
用于探索各种形状的主要工具是形状浏览器。
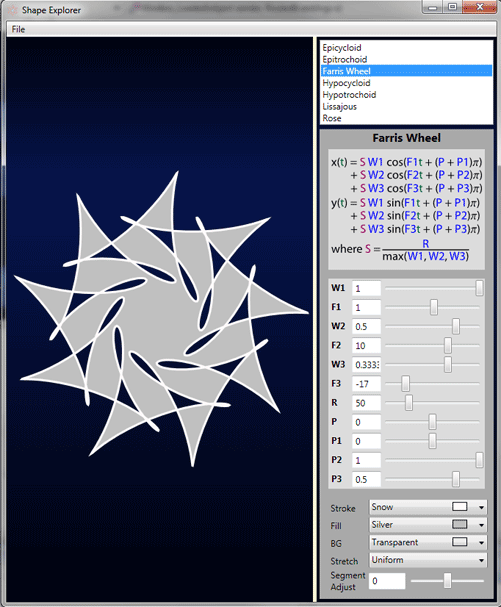
它显示了所选的形状以及用于计算它的公式。可以通过滑块或文本框调整各种参数。您还可以选择填充笔触和背景颜色。
最后,您可以调整用于构建形状的贝塞尔曲线段的数量。SegmentAdjustment 是 2 的幂的指数,该幂乘以形状的预期段数。因此,如果 SegmentAdjustment 是 0,则我们得到 2 的 0 次幂,即 1,或者没有变化。对于 3,我们将有 8 倍的段数,而对于 -2,我们将有 1/4 的数量。增加数量会使形状更好地跟踪曲线,但计算量会增加。(注意:显著降低 SegmentAdjustment 可能导致不可预测的,有时是美丽的曲线。)这似乎很奇怪,但目的是使调整在大小方面不受偏见。如果我使用直接乘法,滑块将从 0 运行到 16,几乎所有的空间都将用于增加段数。这说明了一个重要的观点,即总有多种方法可以选择来组织您的参数。
这都很好,但这并没有完全体现这些形状的特点。为了协助这一点,七种形状中的每一种都有自己的窗口,显示形状网格。这些将与各自的形状一起详细介绍。
外摆线
外摆线是一条古老而著名的曲线。据我们所知,它最早是由罗德斯的希帕克斯(公元前 190-120 年)发现的。它在天文学中通过长期使用的托勒密体系得到了非常实际的应用。从几何上看,外摆线代表一个圆在另一个圆的边缘上滚动而不打滑,这等同于以下方程,其中 R1 是基圆的半径,R2 是滚动圆的半径。

为了几何目的,可以改进此公式。我们不能使用 R1 和 R2,而是可以使用 R1/R2 和 R2 的比例来表示外摆线。R1/R2 或 k 代表形状,R2 代表形状的大小。
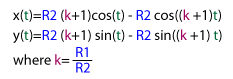
当 k 为有理数时,外摆线才会重复。为了确保形状重复,我选择了 N(分子)和 D(分母)来代替 K 和 R 作为缩放因子。我还添加了一个相位偏移 P,它具有旋转形状的效果。这给出了 Hypocycloid 类中使用的内摆线的以下公式。

在代码中,这对应于
int gcd = Mathematics.NumberTheory.GCD(N, D);//GCD for Greatest common Denominator
double p = (double)N / gcd;
double q = (double)D / gcd;
Double m = (double)p / q - 1;
Function fx = new Function(t => R * m * Math.Cos(t + P) + R * Math.Cos(m * t + P),
t => -R * m * Math.Sin(t + P) - m * R * Math.Sin(m * t + P));
Function fy = new Function(t => R * m * Math.Sin(t + P) - R * Math.Sin(m * t + P),
t => R * m * Math.Cos(t + P) - R * m * Math.Cos(m * t + P));
CyclicCurve c = new CyclicCurve(fx, fy,0,2* Math.PI * q);
有关此代码工作原理的许多详细信息可以在 GraphDisplay:用于绘制函数和曲线的基于贝塞尔的控件 中找到,但我在此处要注意的是
t => R * m * Math.Cos(t + P) + R * Math.Cos(m * t + P
对应于 fx,而
t => R * m * Math.Sin(t + P) - R * Math.Sin(m * t + P)
对应于 fy。此时,您可能会注意到,与其使用一对函数 fx 和 fy,不如将此形状看作是由单个复数函数 z(t) 定义的,其中 fx 是 z 的实部,fy 是 z(t) 的虚部。
![]()
由于我们是通过 t 的完整周期来定义形状的,所以没有理由不能用 D*t 替换 t,这给出了以下有趣的公式。
![]()
因此,我们可以用具有整数修饰符的两个复数指数的和来表示外摆线。演示应用程序还允许您查看外摆线的网格。

外差向曲线
外差向曲线是外摆线的抽象,花了 1600 年才出现。阿尔布雷希特·丢勒(Albrecht Dürer),一位艺术巨匠,于 1525 年写下了这些“蜘蛛线”。从几何上看,外差向曲线定义了与旋转圆不同的半径处的曲线。它是 Spirograph 中一个圆在另一个圆的外部旋转时产生的曲线。(注意,通过使用最外缘的孔,您可以非常接近外摆线,但从技术上讲,它需要精确地在边缘才能得到外摆线而不是外差向曲线。)至于公式,唯一的区别是第二个 R2 被替换为额外的参数 D 来表示附加半径。

与外摆线一样,为了几何目的,可以改进此公式。我们不能使用 R1 和 R2,而是可以使用 R1/R2 和 R2 的比例来表示外差向曲线。R1/R2 或 k 代表形状,R2 代表形状的大小。

此形状使用以下版本的方程来表示外差向曲线。参数 M 用于代替 D,因此当 D=0 时,我们得到外差向曲线。

在代码中,这对应于
int gcd = Mathematics.NumberTheory.GCD(N, D);
double p = (double)N / gcd;
double q = (double)D / gcd;
Double k = (double)p / q;
Function fx = new Function(t => R * ((k + 1) * Math.Cos(t + P) -
Math.Pow(2, M) * Math.Cos((k + 1) * t + P)),
t => -R * ((k + 1) * Math.Sin(t + P) - (k + 1) *
Math.Pow(2, M) * Math.Sin((k + 1) * t + P)));
Function fy = new Function(t => R * (k + 1) * Math.Sin(t + P) - R *
Math.Pow(2, M) * Math.Sin((k + 1) * t + P),
t => R * (k + 1) * Math.Cos(t + P) - R * (k + 1) *
Math.Pow(2, M) * Math.Cos((k + 1) * t + P));
CyclicCurve c = new CyclicCurve(fx, fy, 0, 2 * Math.PI * q);
我们可以看到
t => R * ((k + 1) * Math.Cos(t + P) - Math.Pow(2, M) * Math.Cos((k + 1) * t + P))
对应于 fx,而
t => R * (k + 1) * Math.Sin(t + P) - R * Math.Pow(2, M) * Math.Sin((k + 1) * t + P)
对应于 fy。同样,这可以表示为单个复数函数 z(t),其中 fx 是 z 的实部,fy 是 z(t) 的虚部。
![]()
毫不奇怪,您可以进行相同的替换,用 D*t 替换 t 来获得 t 变量的整数系数。
![]()
外差向曲线显示网格允许您一起查看一组外差向曲线。移动 M 滑块对其外观有显著影响。

内摆线
时间往前推移,内摆线最初是由奥列·罗默(Ole Romer,以光速闻名)在 1674 年研究齿轮时发明/发现的。内摆线可以看作是单个圆在另一个圆内部滚动形成的路径。以下公式很容易证明表示内摆线

然后可以将其写成 R1 和 R2 的比例。

以下版本是用于此形状的版本。请注意,它有一个额外的参数 P 用于形状的整体相位偏移(旋转)。

这些方程在代码中如下所示
int gcd = Mathematics.NumberTheory.GCD(N, D);//GCD for Greatest common Denominator
double p = (double)N / gcd;
double q = (double)D / gcd;
Double m = (double)p / q - 1;
Function fx = new Function(t => R * m * Math.Cos(t + P) + R * Math.Cos(m * t + P),
t => -R * m * Math.Sin(t + P) - m * R * Math.Sin(m * t + P));
Function fy = new Function(t => R * m * Math.Sin(t + P) - R * Math.Sin(m * t + P),
t => R * m * Math.Cos(t + P) - R * m * Math.Cos(m * t + P));
CyclicCurve c = new CyclicCurve(fx, fy,0,2* Math.PI * q);
我们可以看到
t => R * m * Math.Cos(t + P) + R * Math.Cos(m * t + P)
对应于 fx,而
t => R * m * Math.Sin(t + P) - R * Math.Sin(m * t + P)
对应于 fy。同样,这可以表示为单个复数函数 z(t),其中 fx 是 z 的实部,fy 是 z(t) 的虚部。另外,值得注意的是 cos(t) 是偶函数(cos(-t) = cos(t)),而 sin(t) 是奇函数(sin(-t) = -sin(t))。
![]()
如果用 D*t 替换 t,则得到 t 变量的整数系数。
![]()
内摆线显示网格允许您一起查看一组内摆线。

内差向曲线
内差向曲线最早由 Charles de Bovelles(拉丁文名 Carolus Bovillus)于 1501 年构想。它们之所以出名,是因为它们是在 Spirograph 中,当一个小轮子在一个大环内旋转时产生的曲线。它们可以用数学公式表示如下

内差向曲线方程可以用 R1 和 R2 的比例来表示,但还有一个额外的参数 D。如果 D 等于 R2,那么我们就得到一个内摆线。

该形状使用以下版本的内差向曲线方程。参数 M 用于代替 D,因此当 D=0 时,我们得到一个内摆线。

在代码中,这对应于
int gcd = Mathematics.NumberTheory.GCD(N, D);
double p = (double)N / gcd;
double q = (double)D / gcd;
Double k = (double)p / q;
K = k;
Function fx = new Function(t => R * ((k - 1) * Math.Cos(t + P) +
Math.Pow(2, M) * Math.Cos((k - 1) * t + P)),
t => -R * ((k - 1) * Math.Sin(t + P) + (k - 1) *
Math.Pow(2, M) * Math.Sin((k - 1) * t + P)));
Function fy = new Function(t => R * (k - 1) * Math.Sin(t + P) - R *
Math.Pow(2, M) * Math.Sin((k - 1) * t + P),
t => R * (k - 1) * Math.Cos(t + P) - R * (k - 1) *
Math.Pow(2, M) * Math.Cos((k - 1) * t + P));
CyclicCurve c = new CyclicCurve(fx, fy, 0, 2 * Math.PI * q);
我们可以看到
t => R * ((k - 1) * Math.Cos(t + P) + Math.Pow(2, M) * Math.Cos((k - 1) * t + P))
对应于 fx,而
t => R * (k - 1) * Math.Sin(t + P) - R * Math.Pow(2, M) * Math.Sin((k - 1) * t + P)
对应于 fy。
![]()
同样,这可以表示为单个复数函数 z(t),其中 fx 是 z 的实部,fy 是 z(t) 的虚部。
![]()
如果用 D*t 替换 t,则得到 t 变量的整数系数。
内差向曲线显示网格允许您一起查看一组内差向曲线。移动 M 滑块对其外观有显著影响。

菲里斯轮
菲里斯轮将我们带到现在。这条曲线因 F. A. Farris 博士于 1996 年的审美关注而闻名,因此得名。我们已经看到,到目前为止所有曲线都可以写成以下形式
![]()
其中 a 和 b 是整数,A 和 B 是复数。您可以想象将 z(t) 扩展到包含第三项,因此我们有
![]()
这可以直接用 x(t) 和 t(t) 表示为

P 表示整体相位偏移。P、P1、P2、P3 已缩放,因此它们从 -1 到 1 而不是 -PI 到 PI。S 是整体缩放因子,因此 W1、W2、W3 应被视为相对权重。在代码中,这对应于
double maxRadius = Math.Abs(W1) + Math.Abs(W2) + Math.Abs(W3);
Double scaleFactor = R / maxRadius;
double pp1PI = (P + P1) * Math.PI;
double pp2PI = (P + P2) * Math.PI;
double pp3PI = (P + P3) * Math.PI;
Function fx = new Function(t => scaleFactor * (W1 * Math.Cos(F1 * t + pp1PI)
+ W2 * Math.Cos(F2 * t + pp2PI)
+ W3 * Math.Cos(F3 * t + pp3PI)),
t => scaleFactor * (-F1 * W1 * Math.Sin(F1 * t + pp1PI)
- F2 * W2 * Math.Sin(F2 * t + pp2PI)
- F3 * W3 * Math.Sin(F3 * t + pp3PI)));
Function fy = new Function(t => scaleFactor * (W1 * Math.Sin(F1 * t + pp1PI)
+ W2 * Math.Sin(F2 * t + pp2PI)
+ W3 * Math.Sin(F3 * t + pp3PI)),
t => scaleFactor * (F1 * W1 * Math.Cos(F1 * t + pp1PI)
+ F2 * W2 * Math.Cos(F2 * t + pp2PI)
+ F3 * W3 * Math.Cos(F3 * t + pp3PI)));
CyclicCurve c = new CyclicCurve(fx, fy, 0, 2 * Math.PI);
一些因子已被合并以减少算术运算的数量。这是一个比之前更丰富的形状,能够产生各种各样的形式。请注意,对于这个形状,行和列可以改变,因为有三个频率:F1、F2、F3。

李萨如图形
李萨如图形由 Nathaniel Bowditch 于 1815 年发现/发明。Antoine Lissajous 于 1857 年独立重新发现(因此得名)。(有时也称为 Bowditch 曲线。)这些曲线最常在示波器上看到。
![]()
该形状使用以下版本的公式,其中 N 和 D 是整数
![]()
在代码中,这对应于
int gcd = Mathematics.NumberTheory.GCD(Alpha,Beta);
double p = (double)Alpha / gcd;
double q = (double)Beta / gcd;
Function fx = new Function(t => A * Math.Sin(p * t + Delta ),
t => A * p * Math.Cos(p * t + Delta ));
Function fy = new Function(t => B * Math.Sin(q * t),
t => B * q * Math.Cos(q * t ));
CyclicCurve c = new CyclicCurve(fx, fy, 0, 2 * Math.PI );
我们可以看到
t => A * Math.Sin(p * t + Delta )
对应于 fx,而
t => B * Math.Sin(q * t)
对应于 fy。李萨如图形演示展示了该形状能够实现的各种可能性。请注意,更改 Delta 对形状有有趣的影响。

玫瑰曲线
玫瑰曲线由 Luigi Guido Grandi 于 1725 年左右发现/发明。他认为它们看起来像花,因此得名。它们可以用极坐标表示为
![]()
如果 alpha 是有理数,则曲线将闭合。对于该形状,使用以下形式,其中 N 和 D 是整数

该形状在代码中表示为
int gcd = Mathematics.NumberTheory.GCD(N, D);
double p = (double)N / gcd;
double q = (double)D / gcd;
double omega = p / q;
Function fr = new Function(t => A * Math.Sin(omega * t),
t => omega * A * Math.Cos(omega * t));
CyclicPolarCurve rc = new CyclicPolarCurve(fr, 0, 2 * q * Math.PI);
我们可以看到
t => A * Math.Sin(omega * t)
对应于 r,它对应于 fy。玫瑰演示展示了该形状能够实现的各种可能性。

制作您自己的形状
包含的形状代表了可以用数学定义的曲线制作的可能形状的极小一部分。创建其他形状非常容易。在本节中,我将以内摆线为例,因为它展示了所有功能中最简单的。
基础
为了创建形状,必须完成三件事。第一,您必须继承自 FunctionalShapes.FunctionalClosedShapeBase。第二,您必须重写 Curve 属性。在这里,您需要从数学上定义曲线。在本例中,曲线由两个函数 fx 和 fy 组成。Function 类在其构造函数中接受两个委托:一个代表函数的返回值,一个代表导数。有关函数和曲线定义的详细信息,请参阅 GraphDisplay:用于绘制函数和曲线的基于贝塞尔的控件。
protected override Mathematics.BaseClasses.CyclicCurveBase Curve
{
get {
//GCD for Greatest common Denominator
int gcd = Mathematics.NumberTheory.GCD(N, D);
double p = (double)N / gcd;
double q = (double)D / gcd;
Double m = (double)p / q - 1;
Function fx =
new Function(t => R * m * Math.Cos(t + P) + R * Math.Cos(m * t + P),
t => -R * m * Math.Sin(t + P) - m * R * Math.Sin(m * t + P));
Function fy =
new Function(t => R * m * Math.Sin(t + P) - R * Math.Sin(m * t + P),
t => R * m * Math.Cos(t + P) - R * m * Math.Cos(m * t + P));
CyclicCurve c = new CyclicCurve(fx, fy,0,2* Math.PI * q);
K = (double)p / q;
return c;
}
}
第三个要求是定义段属性。这定义了在 SegmentAdjust 调整之前的基数贝塞尔曲线段数。
protected override int Segments()
{
return 200 + N*N + D*D;
}
与动画一起使用 - 依赖属性
现在,如果您愿意花费精力定义一个形状,它很可能不仅仅是为了一个形状,而是为了一个参数化的形状系列。如果使用依赖属性,这将效果更好。这将使您能够使用动画和 WPF 的动态渲染更新。以下是内摆线相位偏移的属性。
public static DependencyProperty PProperty =
DependencyProperty.Register("P", typeof(double), ClassType,
new FrameworkPropertyMetadata(0.0, options,
new PropertyChangedCallback(OnPropChanged)));
[MathParameter("P", -Math.PI, Math.PI, false)]
public double P
{
get
{
return (double)GetValue(PProperty);
}
set
{
SetValue(PProperty, value);
}
}
请注意,有一个 PropertyChangedCallback。它将缓存的几何图形副本置为空。所有影响渲染的依赖属性都需要执行此操作。设置 FrameworkPropertyMetadataOptions 是不够的。
private static void OnPropChanged(DependencyObject d,
DependencyPropertyChangedEventArgs e)
{
Hypocycloid ps = (Hypocycloid)d;
ps.mGeom = null;
}
说到 FrameworkPropertyMetadataOptions,我建议使用以下选项。此外,一旦定义了这样的变量,它就可以在多个依赖属性中使用。
static FrameworkPropertyMetadataOptions options =
FrameworkPropertyMetadataOptions.AffectsRender
| FrameworkPropertyMetadataOptions.AffectsMeasure
| FrameworkPropertyMetadataOptions.AffectsArrange;
我强烈建议在使用具有依赖属性的类系列时使用 ClassType 属性。它很简单,但允许您在不同类之间复制和粘贴。
static Type ClassType
{
get { return typeof(Hypocycloid); }
}
与 Shape Explorer 一起使用 - 自定义属性
您可能想要做的用于测试新形状的一件事是将其用于形状浏览器。在开发本文时,我决定无论如何都不愿意为每个形状单独制作属性编辑器。为了解决这个问题,向该类添加了一个自定义属性,即 MathParameterAttribute。
public sealed class MathParameterAttribute:Attribute
{
/// <summary>
/// The Friendly Name for the Parameter
/// </summary>
public string DisplayName { get; private set; }
/// <summary>
/// The Default Minimum value for the parameter(used by sliders)
/// </summary>
public Double MinValue { get; private set; }
/// <summary>
/// The default Maximum value for the parameter(used by sliders)
/// </summary>
public Double MaxValue { get; private set; }
/// <summary>
/// Is the parameter an integer(used by sliders)
/// </summary>
public bool IsInteger { get; private set; }
/// <summary>
/// Is the parameter Read only
/// </summary>
public bool IsReadOnly { get; set; }
public MathParameterAttribute(String displayName, Double minValue,
Double maxValue, bool isInteger)
{
DisplayName = displayName;
MinValue = minValue;
MaxValue = maxValue;
IsInteger = isInteger;
IsReadOnly = false;
}
public MathParameterAttribute(String displayName)
{
DisplayName = displayName;
IsReadOnly = true;
}
}
它处理我们拥有的两种参数。特别是,该属性支持滑块,为它们提供最小值和最大值以及是否需要限制为整数的信息。请记住,您可以自由地在文本框中输入更大的或更小的值;属性仅影响滑块。常规参数将具有这样的属性
[MathParameter("P", -Math.PI, Math.PI, false)]
此参数的显示名称为 P。(显示名称用于支持名称中的希腊字母和空格。)参数范围从 -PI 到 PI,并且不要求为整数。第二种参数是只读参数。它只需要显示名称。我仍在开发我的属性 UI 框架,因此将来我会给出它应得的解释。
[MathParameter("K" )]
与 GridDemonstration 一起使用 - Clone
您可能还想显示形状网格。要使用 GridDemonstration,必须定义 Clone 方法,基本上就是这样。
public override FunctionalClosedShapeBase Clone()
{
Hypocycloid clonedShape = new Hypocycloid()
{
N = this.N,
D = this.D,
R = this.R,
P =this.P,
Stretch = this.Stretch,
Fill = this.Fill,
Stroke = this.Stroke,
StrokeThickness = this.StrokeThickness,
SegmentAdjustment = this.SegmentAdjustment
};
return clonedShape;
}
包含的形状还为其公式提供了绘图画笔,但我不太确定是否建议在非演示情况下添加它们,因为让它们看起来美观需要一些工作。
结论和后续步骤
我希望这些形状能为您服务。这花了一些功夫,但也很有趣。这些形状,特别是菲里斯轮,玩起来很有趣。即使这样,还有这么多令人兴奋的事情要做。我正在考虑一些进一步的步骤,我希望得到您的建议。
- 制作 Silverlight 版本 - 我认为有合理的可能性可以将其转换为 Silverlight。
- 制作装饰图案 - 大多数数学预备工作都已完成,因此这是一种可能性(装饰图案是大多数货币上看到的描摹式图案)。
- 将形状转换为几何图形源并制作更多装饰方案。我的 Stacked Geometry Brush Factory - CodeProject 的粉丝可能会对此感兴趣。
