65.9K
CodeProject 正在变化。 阅读更多。
Home

函数式编程在数值积分中的应用

Alexandr Stefek
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.67/5 (4投票s)

2014年6月4日

CPOL

5分钟阅读

viewsIcon

21596

downloadIcon

358

本文介绍了如何使用函数式编程以委托 Func 的形式创建不定积分。

目录

  1. 引言
  2. 理论
  3. 代码第一部分
  4. 反导数方法 - 其他实现
  5. 反导数方法不同实现的测试
  6. 反导数方法的用法
  7. 多重积分
  8. 二维积分数值求值
  9. 三维积分数值求值
  10. 结果
  11. 参考文献
  12. 历史

引言

函数式编程被广泛使用和讨论。我第一次接触它仍然记忆犹新。在学习期间，我读了一篇著名的文章 https://codeproject.org.cn/Articles/375166/Functional-programming-in-Csharp，这让我脑海中产生了许多“顿悟”。

因为我做了一些关于数值积分的实验，并且发现了文章 https://codeproject.org.cn/Articles/95073/Using-Nested-Lambda-Functions-to-Implement-Numeric 和 https://codeproject.org.cn/Articles/334308/Numerical-Integration-with-Simpsons-Rule，我决定尝试一些类似的方法，但方式略有不同。

即使这里展示的函数/方法是完全函数的，但它们并不是最优的，您可能会找到更快的实现。但仍然存在一些可用的概念。

因为我真的很喜欢扩展，所以整个代码都在使用它。有关扩展方法的更多解释，您可以查阅 https://codeproject.org.cn/Articles/261639/Extension-Methods-in-NET 或 http://msdn.microsoft.com/en-us/library/bb383977.aspx。

理论

如上所述，本文重点关注数值积分。关于积分的理论可以在维基百科页面 http://en.wikipedia.org/wiki/Integral 和 http://en.wikipedia.org/wiki/Antiderivative 上轻松学到。

方程（图片）摘自 http://en.wikipedia.org/wiki/Integral。

在 C# 语言中，我们希望开发一个函数，其形式声明为

public static Func<double, double> Antiderivative(this Func<double, double> df)

这样用户就可以调用类似

Func<double, double> cos = Math.Cos;
Func<double, double> sin = cos.Antiderivative();

代码第一部分

我实现的第一个方法是反导数函数，其形式非常接近上面代码片段中介绍的形式。实现时，我使用了 Runge-Kutta 方法，它是 辛普森法则 的通用等价物。

/// <summary>
/// limit for numerical computation
/// </summary>
public static double eps = 1e-16;

/// <summary>
/// Numerical antiderivation (integral computation)
/// <para/><see cref="http://en.wikipedia.org/wiki/Antiderivative"/>
/// <para/><see cref="https://www.khanacademy.org/math/integral-calculus/
/// indefinite-definite-integrals/indefinite_integrals/v/antiderivatives-and-indefinite-integrals"/>
/// <para/><see cref="http://www-math.mit.edu/~djk/calculus_beginners/chapter16/section01.html"/>
/// </summary>
/// <example>
/// <code>Func&lt;double, double&gt; sin = Antiderivative(cos, 0, 0, 0.001);</code>
/// </example>
/// <param name="df">derivation</param>
/// <param name="x0">start point</param>
/// <param name="f0">start value f0 = f(x0)</param>
/// <param name="stepSize">step size</param>
/// <returns>integral of input function</returns>
public static Func<double, double> Antiderivative
    (this Func<double, double> df, double x0, double f0, double stepSize)
{
    //save values - state for function which will be returned
    double currentx = x0;
    double currentf = f0;
    double currentdf = df(x0);

    //create function
    return (x) =>
    {
        //not implemented for left values, can be done in future
        if (x < x0)
            throw new ArgumentException("Cannot compute");

        //test relation between currentx (state value) and wanted x | f(x)
        if (currentx > x)
        {
            //reset state if needed
            //this can be improved by values caching this implementation is simplified
            currentx = x0;
            currentf = f0;
            currentdf = df(x0);
        }

        double newLimit = x - stepSize;
        //make loop till the distance is less than deltax
        while (currentx < newLimit)
        {
            //*
            double k1 = stepSize * currentdf; //it is same as k1 = deltax * df(currentx);
            double k2 = stepSize * df(currentx + 0.5 * stepSize);
            double k3 = k2; //it is same as k3 = deltax * df(currentx + 0.5 * deltax);
            currentdf = df(currentx + stepSize);
            double k4 = stepSize * currentdf;
            currentf = currentf + 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);
            //*/

            currentx = currentx + stepSize;
        }

        //now compute last step, if it is needed
        double lastStepSize = x - currentx;
        if (lastStepSize > eps)
        {
            currentf = currentf + lastStepSize * df(currentx);
            currentx = x;
        }
        //and return value, store it for future use
        return currentf;
    };
}

反导数方法 - 其他实现

感谢 Marc Clifton（见文章下方的讨论部分），我包含了反导数方法的其他可能的实现。

首先是避免使用 currentx、currentf 和 currentdf 的实现。AntiderivativePure 方法的完整代码

/// <summary>
/// Numerical antiderivation (integral computation)
/// <para/><see cref="http://en.wikipedia.org/wiki/Antiderivative"/>
/// <para/><see cref="
///https://www.khanacademy.org/math/integral-calculus/indefinite-definite-integrals/
///indefinite_integrals/v/antiderivatives-and-indefinite-integrals"/>
/// <para/><see cref="http://www-math.mit.edu/~djk/calculus_beginners/chapter16/section01.html"/>
/// </summary>
/// <example>
/// <code>Func&lt;double, double&gt; sin = Antiderivative(cos, 0, 0, 0.001);</code>
/// </example>
/// <param name="df">derivation</param>
/// <param name="x0">start point</param>
/// <param name="f0">start value f0 = f(x0)</param>
/// <param name="stepSize">step size</param>
/// <returns>integral of input function</returns>
public static Func<double, double> AntiderivativePure
    (this Func<double, double> df, double x0, double f0, double stepSize)
{
    //create function
    return (x) =>
    {
        //not implemented for left values, can be done in future
        if (x < x0)
            throw new ArgumentException("Cannot compute");

        double currentx = x0;
        double currentf = f0;
        double currentdf = df(x0);

        double newLimit = x - stepSize;
        //make loop till the distance is less than deltax
        while (currentx < newLimit)
        {
            //*
            double k1 = stepSize * currentdf; //it is same as k1 = deltax * df(currentx);
            double k2 = stepSize * df(currentx + 0.5 * stepSize);
            double k3 = k2; //it is same as k3 = deltax * df(currentx + 0.5 * deltax);
            currentdf = df(currentx + stepSize);
            double k4 = stepSize * currentdf;
            currentf = currentf + 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);
            //*/

            currentx = currentx + stepSize;
        }

        //now compute last step, if it is needed
        double lastStepSize = x - currentx;
        if (lastStepSize > eps)
            currentf = currentf + lastStepSize * df(currentx);

        //and return value, store it for future use
        return currentf;
    };
}

其次将展示递归实现。注意表达式

return df.AntiderivativeRecursive(x0, f0, stepSize)(x - stepSize) + delta;

AntiderivativeRecursive 方法的完整代码

/// <summary>
/// Numerical antiderivation (integral computation)
/// <para/><see cref="http://en.wikipedia.org/wiki/Antiderivative"/>
/// <para/><see cref="https://www.khanacademy.org/math/integral-calculus/
/// indefinite-definite-integrals/indefinite_integrals/v/antiderivatives-and-indefinite-integrals"/>
/// <para/><see cref="http://www-math.mit.edu/~djk/calculus_beginners/chapter16/section01.html"/>
/// </summary>
/// <example>
/// <code>Func&lt;double, double&gt; sin = Antiderivative(cos, 0, 0, 0.001);</code>
/// </example>
/// <param name="df">derivation</param>
/// <param name="x0">start point</param>
/// <param name="f0">start value f0 = f(x0)</param>
/// <param name="stepSize">step size</param>
/// <returns>integral of input function</returns>
public static Func<double, double> AntiderivativeRecursive
    (this Func<double, double> df, double x0, double f0, double stepSize)
{
    //create function
    return (x) =>
    {
        //not implemented for left values, can be done in future
        if (x < x0)
            throw new ArgumentException("Cannot compute");

        if (x - x0 < stepSize)
        {
            double cstep = x - x0;
            double k1 = cstep * df(x0);
            double k2 = cstep * df(x0 + 0.5 * cstep);
            double k3 = k2; //it is same as k3 = cstep * df(x0 + 0.5 * cstep);
            double k4 = cstep * df(x0 + cstep);
            double currentf = f0 + 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);

            return currentf;
        }
        else
        {
            double k1 = stepSize * df(x - stepSize);
            double k2 = stepSize * df(x - 0.5 * stepSize);
            double k3 = k2; //it is same as k3 = stepSize * df(x - 0.5 * stepSize);
            double k4 = stepSize * df(x);
            double delta = 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);

            return df.AntiderivativeRecursive(x0, f0, stepSize)(x - stepSize) + delta;
        }
    };
}

最后是（至少在这个阶段）AntiderivativeEx 方法的实现

/// <summary>
/// Numerical antiderivation (integral computation)
/// <para/><see cref="http://en.wikipedia.org/wiki/Antiderivative"/>
/// <para/><see cref="https://www.khanacademy.org/math/
/// integral-calculus/indefinite-definite-integrals/indefinite_integrals/v/antiderivatives-and-indefinite-integrals"/>
/// <para/><see cref="http://www-math.mit.edu/~djk/calculus_beginners/chapter16/section01.html"/>
/// </summary>
/// <example>
/// <code>Func&lt;double, double&gt; sin = Antiderivative(cos, 0, 0, 0.001);</code>
/// </example>
/// <param name="df">derivation</param>
/// <param name="x0">start point</param>
/// <param name="f0">start value f0 = f(x0)</param>
/// <param name="stepSize">step size</param>
/// <returns>integral of input function</returns>
public static Func<double, double> AntiderivativeEx
    (this Func<double, double> df, double x0, double f0, double stepSize)
{
    return (x) => df.AntiderivativeExH(x0, f0, stepSize)(x, df(x));
}

private static Func<double, double, double> AntiderivativeExH
    (this Func<double, double> df, double x0, double f0, double stepSize)
{
    //create function
    return (x, dfx) =>
    {
        //not implemented for left values, can be done in future
        if (x < x0)
            throw new ArgumentException("Cannot compute");

        if (x - x0 < stepSize)
        {
            double cstep = x - x0;
            double k1 = cstep * df(x0);
            double k2 = cstep * df(x0 + 0.5 * cstep);
            double k3 = k2; //it is same as k3 = cstep * df(x0 + 0.5 * cstep);
            double k4 = cstep * dfx; //it is same as k4 = cstep * df(x0 + cstep);
            double currentf = f0 + 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);

            return currentf;
        }
        else
        {
            double dfxmh = df(x - stepSize);
            double k1 = stepSize * dfxmh;
            double k2 = stepSize * df(x - 0.5 * stepSize);
            double k3 = k2; //it is same as k3 = stepSize * df(x - 0.5 * stepSize);
            double k4 = stepSize * dfx;
            double delta = 1 / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4);

            return df.AntiderivativeExH(x0, f0, stepSize)(x - stepSize, dfxmh) + delta;
        }
    };
}

最后一个实现使用了函数 Func<double, double, double> ，它可以容纳已经计算出的 dfxm = df(x - stepSize) 值。一旦计算出该值，就会与其他评估共享（参见上面代码中的最后一个表达式 df.AntiderivativeExH(x0, f0, stepSize)(x - stepSize, dfxmh)）。

反导数方法不同实现的测试

当然，实现方式存在差异，一个好问题是这些差异会对性能产生多大的影响？为了能够回答这个问题，我准备了一个测试，将观察两个方面——调用计数和时间消耗。

测试代码如下

private void AntiderivativePerformanceTest()
{
    int calls = 0;
    Func<double, double> cos = (x) =>
    {
        calls++;
        return Math.Cos(x);
    };

    Func<double, double> sin = cos.Antiderivative(0, 0, 0.01);
    Func<double, double> sinB = cos.AntiderivativePure(0, 0, 0.01);
    Func<double, double> sinC = cos.AntiderivativeRecursive(0, 0, 0.01);
    Func<double, double> sinD = cos.AntiderivativeEx(0, 0, 0.01);

    int cycles = 1000;
    calls = 0;
    int start = Environment.TickCount;
    for (int i = 0; i < cycles; i++)
        for (double x = 0; x < Math.PI; x = x + 0.1)
        {
            double sinValueI = sin(x);
        }
    int elapsed = Environment.TickCount - start;
    Msg(string.Format("Antiderivative: {0}ms, calls: {1}", elapsed, calls));

    calls = 0;
    start = Environment.TickCount;
    for (int i = 0; i < cycles; i++)
        for (double x = 0; x < Math.PI; x = x + 0.1)
        {
            double sinValueI = sinB(x);
        }

    elapsed = Environment.TickCount - start;
    Msg(string.Format("AntiderivativePure: {0}ms, calls: {1}", elapsed, calls));

    calls = 0;
    start = Environment.TickCount;
    for (int i = 0; i < cycles; i++)
        for (double x = 0; x < Math.PI; x = x + 0.1)
        {
            double sinValueI = sinC(x);
        }
    elapsed = Environment.TickCount - start;
    Msg(string.Format("AntiderivativeRecursive: {0}ms, calls: {1}", elapsed, calls));

    calls = 0;
    start = Environment.TickCount;
    for (int i = 0; i < cycles; i++)
        for (double x = 0; x < Math.PI; x = x + 0.1)
        {
            double sinValueI = sinD(x);
        }
    elapsed = Environment.TickCount - start;
    Msg(string.Format("AntiderivativeEx: {0}ms, calls: {1}", elapsed, calls));
}

所有实现都用于评估积分函数的 3200 个值。这些测试结果如下

Antiderivative: 46ms, calls: 642999
AntiderivativePure: 750ms, calls: 9974000
AntiderivativeRecursive: 1625ms, calls: 14919000
AntiderivativeEx: 1235ms, calls: 9978000

正如我们所读到的，Antiderivative 方法最快（46 毫秒），df 函数的调用次数最少（643k）。如果我们避免递归实现和状态变量（currentx、currentf 和 currentdf）的使用，我们将得到 750 毫秒和近一百万次调用（0.997M）。

有两个实现使用了递归调用 AntiderivativeRecursive 和 AntiderivativeEx。AntiderivativeEx 比 AntiderivativeRecursive 更快（1235 毫秒）并且调用次数更少（0.998M）。由于优化了 df 函数的调用，这两个方面都有所改进。正如您在相应的代码（AntiderivativeExH 方法）中所看到的，这种优化是通过在递归调用之间共享导数值来实现的。

反导数方法的用法

为了测试 Antiderivative 方法，我选择了 sin(x) 和 cos(x) 的测试。

private void AntiderivativeTest()
{
    Func<double, double> cos = Math.Cos;
    Func<double, double> sin = cos.Antiderivative(0, 0, 0.01);
    for (double x = 0; x < Math.PI; x = x + 0.1)
    {
        double sinValueI = sin(x);
        double sinValue = Math.Sin(x);
        double delta = sinValue - sinValueI;
        Msg(string.Format("x = {0:F6}, Math.Sin(x) = {1:F6}, sin(x) = {2:F6}, delta = {3:F6}", x, sinValue, sinValueI, delta));
    }
}

方法的结果是

x = 0.000000, Math.Sin(x) = 0.000000, sin(x) = 0.000000, delta = 0.000000
x = 0.100000, Math.Sin(x) = 0.099833, sin(x) = 0.099833, delta = 0.000000
x = 0.200000, Math.Sin(x) = 0.198669, sin(x) = 0.198669, delta = 0.000000
x = 0.300000, Math.Sin(x) = 0.295520, sin(x) = 0.295520, delta = 0.000000
x = 0.400000, Math.Sin(x) = 0.389418, sin(x) = 0.389418, delta = 0.000000
x = 0.500000, Math.Sin(x) = 0.479426, sin(x) = 0.479426, delta = 0.000000
x = 0.600000, Math.Sin(x) = 0.564642, sin(x) = 0.564642, delta = 0.000000
x = 0.700000, Math.Sin(x) = 0.644218, sin(x) = 0.644218, delta = 0.000000
x = 0.800000, Math.Sin(x) = 0.717356, sin(x) = 0.717356, delta = 0.000000
x = 0.900000, Math.Sin(x) = 0.783327, sin(x) = 0.783327, delta = 0.000000
x = 1.000000, Math.Sin(x) = 0.841471, sin(x) = 0.841471, delta = 0.000000
x = 1.100000, Math.Sin(x) = 0.891207, sin(x) = 0.891207, delta = 0.000000
x = 1.200000, Math.Sin(x) = 0.932039, sin(x) = 0.932039, delta = 0.000000
x = 1.300000, Math.Sin(x) = 0.963558, sin(x) = 0.963558, delta = 0.000000
x = 1.400000, Math.Sin(x) = 0.985450, sin(x) = 0.985450, delta = 0.000000
x = 1.500000, Math.Sin(x) = 0.997495, sin(x) = 0.997495, delta = 0.000000
x = 1.600000, Math.Sin(x) = 0.999574, sin(x) = 0.999574, delta = 0.000000
x = 1.700000, Math.Sin(x) = 0.991665, sin(x) = 0.991665, delta = 0.000000
x = 1.800000, Math.Sin(x) = 0.973848, sin(x) = 0.973848, delta = 0.000000
x = 1.900000, Math.Sin(x) = 0.946300, sin(x) = 0.946300, delta = 0.000000
x = 2.000000, Math.Sin(x) = 0.909297, sin(x) = 0.909297, delta = 0.000000
x = 2.100000, Math.Sin(x) = 0.863209, sin(x) = 0.863209, delta = 0.000000
x = 2.200000, Math.Sin(x) = 0.808496, sin(x) = 0.808496, delta = 0.000000
x = 2.300000, Math.Sin(x) = 0.745705, sin(x) = 0.745705, delta = 0.000000
x = 2.400000, Math.Sin(x) = 0.675463, sin(x) = 0.675463, delta = 0.000000
x = 2.500000, Math.Sin(x) = 0.598472, sin(x) = 0.598472, delta = 0.000000
x = 2.600000, Math.Sin(x) = 0.515501, sin(x) = 0.515501, delta = 0.000000
x = 2.700000, Math.Sin(x) = 0.427380, sin(x) = 0.427380, delta = 0.000000
x = 2.800000, Math.Sin(x) = 0.334988, sin(x) = 0.334988, delta = 0.000000
x = 2.900000, Math.Sin(x) = 0.239249, sin(x) = 0.239249, delta = 0.000000
x = 3.000000, Math.Sin(x) = 0.141120, sin(x) = 0.141120, delta = 0.000000
x = 3.100000, Math.Sin(x) = 0.041581, sin(x) = 0.041581, delta = 0.000000

一旦我们得到了创建反导数函数的方法，我们就可以用它来数值求解定积分

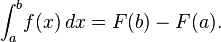
方程（图片）摘自 http://en.wikipedia.org/wiki/Integral。

所以 C# 中的方法可以这样写

/// <summary>
/// Takes function and evals f(to) - f(from)
/// </summary>
/// <param name="f"></param>
/// <param name="from"></param>
/// <param name="to"></param>
/// <returns></returns>
public static double IntervalEval(this Func<double, double> f, double from, double to)
{
    double l = f(from);
    double h = f(to);
    return h - l;
    //abit better than
    //return f(to) - f(from);
    //especially in usage with Antiderivative function
}

/// <summary>
/// Calculates integral of fx over interval where a is low bound and b is high bound
/// <see cref="http://en.wikipedia.org/wiki/Integral"/>
/// </summary>
/// <param name="fx">function to integrate</param>
/// <param name="a">low bound</param>
/// <param name="b">high bound</param>
/// <param name="stepSize">step size</param>
/// <returns>Integral value</returns>
public static double Integral(this Func<double, double> fx, double a, double b, double stepSize)
{
    return fx.Antiderivative(a, 0, stepSize).IntervalEval(a, b);
}

Interval 方法是为了简化方程右侧的区间求值。请注意，Integral 方法的主体只有一行。

在实现这个阶段，问题“二维积分怎么办？”会出现。

多重积分

多重积分在维基百科上有讨论，请参见 http://en.wikipedia.org/wiki/Integral#Extensions - 多重积分 或 http://en.wikipedia.org/wiki/Multiple_integral。多重积分的一种非常常见的形式是二维和三维积分，可用于面积或体积计算。

二维积分数值求值

二维积分可以通过使用以下方程来计算

方程（图片）摘自 http://en.wikipedia.org/wiki/Multiple_integral。

/// <summary>
/// Create function f(y) from f(x, y) in form f(const x, y)
/// </summary>
/// <param name="fxy">function f(x, y)</param>
/// <param name="x">const x</param>
/// <returns>function f(y)</returns>
public static Func<double, double> FixateX(this Func<double, double, double> fxy, double x)
{
    return (y) => fxy(x, y);
}

/// <summary>
/// Calculates 2D integral of f over shape defined by lowx, highx, lowy(x) and highy(x) bounds.
/// </summary>
/// <param name="fxy">function to integrate</param>
/// <param name="lowX">x low bound</param>
/// <param name="highX">x high bound</param>
/// <param name="lowY">y(x) func low bound</param>
/// <param name="highY">y(x) func high bound</param>
/// <param name="stepSize">step size</param>
/// <returns>Integral value</returns>
public static double Integral(this Func<double, double, double> fxy, 
double lowX, double highX, Func<double, double> lowY, Func<double, double> highY, double stepSize)
{
    Func<double, double> helperFunc = 
        (cx) => fxy.FixateX(cx).Integral(lowY(cx), highY(cx), stepSize);
    return helperFunc.Integral(lowX, highX, stepSize);
}

FixateX 方法是为了简化。如果省略这个通用方法，实现可以缩短。即使 Integral 方法的主体可以写成一行，但两个表达式的实现更容易理解（也许再多一行会更优化）。

此方法的测试可以这样写

//calculate circle with radius r area (Pi*r*r)
private double Circle(double r)
{
    Func<double, double, double> fxy = (x, y) => 1;
    Func<double, double> yboundLow = (x) => -Math.Sqrt(r * r - x * x);
    Func<double, double> yboundHigh = (x) => Math.Sqrt(r * r - x * x);

    double result = 0;
    result = fxy.Integral(-r, r, yboundLow, yboundHigh, 0.01);
    return result;
}

private void I2DTest()
{
    Msg("Circle = " + Circle(1));
    Msg("Expected : " + Math.PI);
}

I2DTest 的结果是

Circle = 3.14143024919302
Expected : 3.14159265358979

现在三维积分呢？当然！让我们来做吧！

三维积分数值求值

对于三维积分，我们可以使用一个非常相似的方程（与二维比较）

方程摘自 http://en.wikipedia.org/wiki/Multiple_integral。

C# 实现可以是这样的

/// <summary>
/// Create function f(y, z) from f(x, y, z) in form f(const x, y, z)
/// </summary>
/// <param name="fxy">function f(x, y, z)</param>
/// <param name="x">const x</param>
/// <returns>function f(y, z)</returns>
public static Func<double, double, double> FixateX
    (this Func<double, double, double, double> fxyz, double x)
{
    return (y, z) => fxyz(x, y, z);
}

/// <summary>
/// Calculates 3D integral of f over volume defined 
/// by lowx, highx, lowy(x), highy(x), lowz(x, y) and highz(x, y) bounds.
/// </summary>
/// <param name="fxyz">function to integrate</param>
/// <param name="lowX">x low bound</param>
/// <param name="highX">x high bound</param>
/// <param name="lowY">y(x) func low bound</param>
/// <param name="highY">y(x) func high bound</param>
/// <param name="lowZ">z(x, y) func low bound</param>
/// <param name="highZ">z(x, y) func high bound</param>
/// <param name="stepSize">step size</param>
/// <returns>Integral value</returns>
public static double Integral(this Func<double, double, double, double> fxyz,
    double lowX, double highX, Func<double, double> lowY, Func<double, 
    double> highY, Func<double, double, double> lowZ, Func<double, 
    double, double> highZ, double stepSize)
{
    Func<double, double> helperFunc = 
        (cx) => fxyz.FixateX(cx).Integral(lowY(cx), 
        highY(cx), lowZ.FixateX(cx), highZ.FixateX(cx), stepSize);
    return helperFunc.Integral(lowX, highX, stepSize);
}

FixateX 方法是为了简化。如果省略这个通用方法，实现可以缩短。即使 Integral 方法的主体可以写成一行，但两个表达式的实现更容易理解（也许再多一行会更优化）。真的和二维是一样的说法……

此方法的测试可以这样写

//calculate volume of sphere with radius r (4/3*Pi*r*r*r)
private double Sphere(double r)
{
    Func<double, double, double, double> fxyz = (x, y, z) => 1;
    Func<double, double> yboundLow = (x) => -Math.Sqrt(r * r - x * x);
    Func<double, double> yboundHigh = (x) => Math.Sqrt(r * r - x * x);
    Func<double, double, double> zboundLow = (x, y) => -Math.Sqrt(r * r - x * x - y * y);
    Func<double, double, double> zboundHigh = (x, y) => Math.Sqrt(r * r - x * x - y * y);

    double result = 0;
    result = fxyz.Integral(-r, r, yboundLow, yboundHigh, zboundLow, zboundHigh, 0.01);
    return result;
}

private void I3DTest()
{
    Msg("Sphere = " + Sphere(1).ToString());
    Msg("Expected : " + 4 * Math.PI / 3);
}

I3DTest 的结果是

Sphere = 4.18857816178346
Expected : 4.18879020478639

结果

在引言部分，曾警告过算法的优化性。是的，这个实现的速度评估不是最优的。但为什么有时不创造一些“优雅”的东西呢？这项工作帮助我更熟悉了函数式编程。

参考文献

历史

  • 2014年6月4日 首次实现（从零开始）
  • 2014年6月11日 根据讨论更新（并修复了 bug - 提高了精度）
© . All rights reserved.