C++ 中半群的高效表示

• 下载 semigroup_performance.zip - 3.1 KB
• 下载 bp_tree_bin_op.zip - 11 KB
• 下载 semigroup_demo.zip - 2.8 KB

摘要

我们讨论了结合二元运算的推广，这导致了基于一个增强型B+树类模板的C++中数学半群的有效表示。这种表示对于一系列实际应用非常有用，包括快速计算数据集的总和、最小值/最大值和统计参数。我们还简要比较了SQL查询中使用的聚合树。

布局

• 引言
• 基本算法的推广
• 高级数据结构和算法设计
• 半群
• STL工具
• 基本应用
• 与聚合树的比较
• 性能
• Using the Code
• 参考文献

引言

平衡搜索树具有众多的实际应用，因为它们比数组和链表提供更广泛的有效搜索和更新操作。如果线性数据结构至少有一个用户算法所需的低效操作，则会造成性能瓶颈。

平衡树的增强变体提供了额外的有效操作和算法，从而扩展了这些树的应用领域。例如，传统的平衡搜索树仅有效支持有序容器：std::set, std::multiset, std::map 和 std::multimap。增强树不仅适用于实现有序容器，也适用于实现无序容器。在某些应用中，这些容器的性能优于标准容器 std::vector 和 std::list。增强树甚至可以用于海量数据集的快速求和。

在这里，我们讨论了数学半群的表示，它支持各种类型的结合二元运算，包括不相关的运算，例如算术加法和最小值的选择。该表示被定义为一个增强B+树的类模板，它以一个结合二元运算作为参数。通过将特定二元运算的函数对象作为模板参数传递，该类模板可以轻松地在算法中使用。在不损失效率的情况下实现了高度的通用性，这是通用库设计中的一个重要标准。

数学半群的基本性质使其在各种重要应用中都具有潜在的实用价值。然而，只有在编程语言中正确实现这个概念，才能使其在实践中发挥计算能力。通过高效计算数据集统计参数的例子，说明了所开发表示的优点，并将其与SQL查询中使用的聚合树的功能进行了比较。

基本算法的推广

由于其复杂性，增强树属于高级数据结构。为了专注于主要思想而不是实现细节，使用简化版的数据结构是合理的。通过考虑基本算法和数据结构的变体，可以更容易地理解通用表示的某些方面。因此，我们从以下问题开始讨论：如何使用C++标准函数std::accumulate()在一个元素范围内找到最小值？

解决方案涉及选择两个值中最小值的二元函数对象。

template < class _Value > 
struct min_value : public std::binary_function < _Value , _Value , _Value > 
{
    _Value  operator ( ) ( const _Value &  x , const _Value &  y ) const 
    {
        _Value  res = ( y < x ) ? y : x ; 
        return  res ; 
    } 
} ;

这个函数对象的使用与 std::plus 的使用不同。一般来说，默认值对于最小值函数来说是不安全的，因此我们使用范围内的第一个元素来初始化结果值。

int        val_init = *pos_a ; 
int        val_acc  = 0 ; 
min_value<int>  bop_min ; 
val_acc = std::accumulate ( pos_a+1 , pos_b , val_init , bop_min ) ;

这个解决方案在实践中是否有用？在C++代码中，这不太可能。C++标准库提供了函数std::min_element()，它对于所提出的任务来说是最佳的。该函数返回一个指向范围内第一个最小值的迭代器。

int     val_min = *(min_element(pos_a, pos_b)) ;    

尽管如此，比较两种寻找最小值的方法值得更详细的讨论。函数对象min_value实现了标准函数对象std::plus的接口，而不是函数std::min()。该示例表明，使用std::accumulate()的方法比使用函数std::min_element()的方法更通用。这个重要的结论源于std::accumulate()函数可以在用户算法中替代std::min_element()函数，但反之则不然。例如，std::min_element()不能与加法和乘法等操作一起使用。基于std::accumulate()函数的解决方案是使用以二元操作为参数的通用算法的示例。使用略有不同的二元函数对象的相同算法可以找到最大值。

函数std::accumulate()的通用化能力可能不明显。STL对算法的分类将所讨论的标准函数分配到不同的类别。这些函数在不同的文件中声明：<numeric>和<algorithm>。然而，分析表明，这两个库函数都实现了本质上相同的顺序处理算法，但使用不同类型的函数对象。比较函数对象返回一个bool，而加法函数对象返回一个值类型的副本对象。bool的小尺寸使得使用函数std::min_element()的代码比使用函数std::accumulate()的代码稍微更高效。同时，二元函数对象的这种差异导致了函数std::min_element()通用性的丧失。

在大规模应用中，函数 std::min_element() 略高的性能优势可能会适得其反。简单的顺序搜索具有线性计算复杂度，这对于高性能应用来说是不可接受的。顺序处理的线性低效率可以通过使用更高级的算法来解决，这些算法使用相对复杂的数据结构，例如平衡树。如果现有库中提供了替代方案，则实现此类解决方案的成本通常不会太高。但是，如果解决方案需要开发新的数据结构和算法，成本会急剧增加。

例如，假设我们有一个高级数据结构，它提供了高效的搜索和更新操作，并且能够使用优于 std::accumulate() 函数的算法在对数时间内计算许多统计参数。这种数据结构的常见情况是，实现限制了某些算法的性能。特别是，该数据结构存在低效率问题，即在给定范围内查找最小值和最大值的操作具有线性计算复杂度。

解决此问题的一种典型方法是在用户算法中添加一个容器，例如 std::multiset 或 std::set。这个额外的容器可以提供对有序元素进行必要的高效搜索。在实践中，这种方法的实现可能具有挑战性，因为它必须同步不同容器上的操作。这种方法的另一个问题是，对其中一个支持容器的低效操作会显著影响用户算法的性能。

所讨论的以二元运算为参数的通用算法示例展示了如何重用在高级数据结构的类模板中实现的有效算法。这种方法仅需少量成本来开发一个表示特定二元运算的函数对象，并且此成本不取决于已实现数据结构的复杂性。这种方法提供了一个显著优势，即用户算法中所需的所有操作都由一个数据结构支持。这种方法的成功取决于此类数据结构的设计和实现质量。

高级数据结构和算法设计

任何顺序算法都需要线性时间，因为要处理范围内的每个元素。为了提高算法的性能，有必要减少计算操作的数量。当数据集的元素被分组并且算法在为每个组预先计算的值上操作时，这是可能的。随着数据集的增长和算法性能变得不可接受，该方法可以反复应用，每次都对最近预先计算的值进行分组。

适用于实现这种性能改进方法的数据结构之一是层级链接的B+树，它在内部节点中存储预计算数据。它支持两种快速求和算法的变体，更详细的讨论请参见[1]。在二元运算推广的背景下，特别令人感兴趣的是计算任何连续元素范围内的结果的算法。该算法的原理图示如下图所示，用于快速求和。作为比较，此图还显示了链表中的标准顺序求和。第一个操作是通过赋值运算符进行的初始化。

图1：使用最深层两个节点之间最短路径的快速求和算法示意图。

该数据结构具有一个有趣的特性，这对于提高顺序处理算法的性能很有用。最深层两个相距遥远的节点之间的路径通过内部节点比通过最深层节点更短。使用最短路径（不一定是唯一的）的计算算法对于这种数据结构来说是最有效的。它对路径上节点中存储的数据执行最少数量的二元操作，并获得与访问最深层每个节点的标准顺序算法相同的结果。

存储在此类数据结构内部节点中的值是使用用户算法提供的二元操作计算的。父节点存储应用于所有子节点中存储的值的二元操作的结果。通过这种方式，二元操作构建了自己的值子结构。

此外，还有一种特殊的子结构，可以针对任何类型的增强型B+树实现，甚至不需要用户提供的二元操作。这是存储容器元素的B+树外部节点的计数子结构。

图2：外部节点和容器元素的计数子结构。底线显示了外部节点的秩。

计数子结构使增强型B+树能够高效地表示数学序列。与任何其他特定于用户二元操作的子结构不同，计数的值不依赖于最深层节点中元素的值。计数子结构提供了对由其秩指定的元素的有效访问，无论容器中的元素是否有序。它支持在最深层任意两个节点之间快速计算距离和元素数量。它可用于实现下标运算符和随机访问迭代器。内部节点中的计数也用于通过二元操作泛化的高效算法中查找最短路径。由于这些序列操作和算法的重要性，计数子结构受到每种增强型B+树变体的支持。

支持快速求和算法的增强型B+树变体，在内部节点中同时存储元素计数和其子节点的总和值，这等于该内部节点为根的子树中所有元素值的总和。下图仅显示总和子结构。

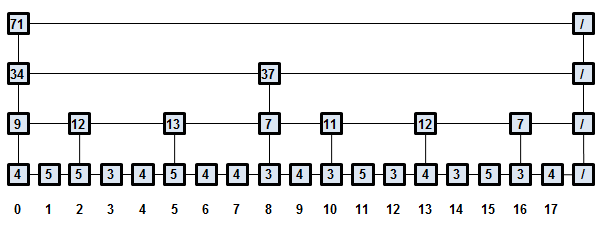
图3：容器元素值总和的子结构。

总和子结构看起来像计数子结构的一个更通用的变体。当最深层的每个节点都存储整数值1时，这些数据结构变得相同。然而，这个事实并没有使计数数据变得不必要。这些子结构相似只是因为它们是用相同的加法运算应用于相同类型的值来构建的。对于其他类型的容器元素和关联二元运算，计数子结构和特定于用户提供的二元运算的子结构之间的差异可能要深刻得多。

下图说明了支持高效计算最小值的增强型B+树的这个事实。它在内部节点中具有值子结构，这与前面讨论的两种子结构都大不相同。

图4：容器元素最小值的子结构。

该子结构使用选择两个值中最小值的二元操作来构建。这种数据结构的独特之处在于堆序：父节点中的值是其子节点中存储值的最小值。堆序属性使该数据结构能够支持对整个数据集的优先级队列的有效操作。在这方面，B+树提供了与基于完全二叉树的二叉堆相同的功能。

然而，与二叉堆相比，增强型B+树提供了额外的范围操作，其运行时间与范围内的元素数量呈对数关系。这种增强型B+树的扩展功能由基于元素计数子结构和最短路径算法的序列表示支持。范围内最小值的快速计算使用与快速求和算法相同的路径（参见图1）。唯一的区别是，它使用选择两个值中最小值的二元操作，而不是加法。

半群

数学概念的选择是数据结构和算法开发中的一个重要设计步骤。它影响它们在用户算法中的有效性和实现的便利性。对于结合不相关操作（如加法和两个值的最小值）的广义数据结构和算法变体，这种选择尤其具有挑战性。

从数学角度来看，幺半群是一个高级概念，足以解决实践中的各种问题。幺半群的定义为一个集合配备了一个结合二元运算和一个单位元。对于大多数二元运算，如加法和乘法，在编程语言中支持单位元并不是一个严重的复杂问题。然而，两个值的最小值和最大值与其他二元运算有很大不同。它们的单位元具有无限值。对于广义编程实现，这是一个非平凡的要求，因为存在可移植性和类型转换问题。

为了提供更高级别的安全性并避免与无限值表示相关的复杂性，增强型B+树的类模板建模了一个半群而不是幺半群。 半群是一个更通用的数学概念，从实现角度来看也更简单。半群不需要支持单位元。它仅由一个集合和一个结合二元运算指定。在文件"bp_tree_bin_op.hpp"中实现的半群，即class bp_tree_bin_op，不使用任何具有无限值的哨兵，也不对用户算法中可以表示单位元的特定值做任何假设。

主接口成员函数bp_tree_bin_op::reduce()的声明与函数std::accumulate()的声明不同。新函数仅要求序列中有效非空的元素范围。不使用初始值是为了避免最小值/最大值二元操作中默认值引起的细微错误。结果值用指定范围内第一个元素的值初始化。此接口函数的二元操作函数对象作为容器匹配模板参数的参数传递。

class bp_tree_bin_op仅用一种二元运算类型进行参数化，这是实现通用性和效率的重要因素。专门算法可以利用特定于应用的特性，提供比通用算法更好的性能。例如，可以使用运行时间恒定的方法获得序列中任意数量的连续元素的和。这种快速方法将序列元素的预计算部分和sum(0, k)存储在额外的容器（例如数组）中，并使用以下公式计算所需的和

sum(m, n) = sum(0, n) - sum(0, m) ; 

该算法的高效率是以额外的存储空间和更新操作性能降低为代价实现的。同样重要的是，该方法利用了减法，它是加法的逆运算。将所述快速方法推广到计算任意数量连续元素的最小值是不可能的，因为最小值没有逆运算。

半群的定义广泛涵盖了许多类型的数学对象，并且不指定时间和空间要求。某些类型的数学对象的编程表示可能非常复杂。操作的时间和空间效率对于使表示在实践中实用至关重要。本文讨论的增强B+树支持的高性能算法要求二元操作的计算复杂度为常数。外部节点中的元素和内部节点中的预计算值应使用恒定的空间量。

一个不满足这些要求的对象示例是带有连接二元操作的字符串。字符串通常由使用可变内存量的容器表示。从技术上讲，增强型B+树可以在外部节点中存储字符串作为容器的元素。这种增强树的使用效率不高，因为内部节点中的预计算字符串会使用大量内存。高效的字符串操作由相对简单的B+树提供，该B+树增加了元素计数并实现了字符序列，参见项目STL Extensions中的“示例”部分。这种增强型B+树的变体类似于rope数据结构。字符串连接可以通过其中一个具有对数运行时间的splice()成员函数执行。

一个对实现半群表示的高质量很重要的实际问题是容器元素数据类型的选择。它取决于结合二元运算的安全性。某些操作，例如两个值的最小值/最大值、逻辑或、与，不会引起任何复杂问题。如果操作数的值有效，则结果也有效，因为它等于其中一个操作数的值。另一方面，加法和乘法操作可能会产生超出数据类型范围的结果值。为了解决这个问题，C++提供了各种内置类型，并允许程序员开发用户定义类型以满足应用程序特定需求。

整数类型和基于整数类型的用户定义类型最适合实现半群。它们的主要限制是由大规模应用中的溢出和下溢错误引起的。用浮点类型替换整数类型可能是明智的，但存在另一个潜在问题，即使用后者的计算会受到数值误差的影响。严格来说，浮点数据类型不满足二元运算结合律的要求。即使在三个变量的简单情况下，也不能保证浮点计算的和(a + b) + c会提供与a + (b + c)相同的结果。随着值的数量增加，计算结果变得不那么精确。数值误差是导致树内部节点中与增强数据相关的不变式可能失效的复杂性的原因。基于浮点类型的半群必须在应用程序可接受的范围内控制精度。文件"semigroup_demo.cpp"中的示例不使用浮点数据类型，以避免数值误差问题。

STL工具

本讨论主要侧重于通过二元运算对算法进行泛化。除此之外，还需要提及的是，增强型B+树提供了各种高效的搜索和更新操作，使其能够支持C++标准容器的接口：vector, list, deque, set, multiset, map和multimap。基于这些树的容器扩展了标准库的框架。它们可以在复杂算法中作为简单的即插即用替代品，以避免标准容器性能低下带来的低效率。有关基于增强型B+树的STL扩展的更详细描述，请参阅项目STL Extensions。

之前开发的增强型B+树之一（class bp_tree_array_acc）支持快速求和算法，但它不适用于表示半群或幺半群。主要问题是其实现要求值类型提供四个C++运算符：+,+=,-,-=。新版增强型B+树（附件文件"bp_tree_bin_op.hpp"中的class bp_tree_bin_op）通过使用单个结合二元运算解决了这个问题。在这方面，新树提供了更高的通用性，扩展了其前身的应用程序范围，并允许基于新容器和算法开发更强大的STL工具。

新增强型B+树的优势可以通过优先级队列的表示来说明。使用数组中完全二叉树的二叉堆存在最大容量限制。基于增强型B+树的表示避免了这一限制。此外，它还支持序列并在容器内的任何位置提供各种插入和擦除操作。对此类序列的每次更新操作都维护着最深层元素的相对顺序和内部节点的堆序。

由于新的增强型B+树是演示版本，它只提供了其前身的一小部分操作。以前开发的所有符合STL的成员函数都可以在新类中实现，如果需要的话。这些函数和其他操作的计算复杂度将是相同的。然而，前一个增强型B+树版本在某些操作上可能具有更好的绝对运行时间，因为其实现利用了逆操作。

基本应用

使用增强数据结构解决问题有两种方法。第一种方法是，用户算法根据需要构造和使用尽可能多的增强型B+树，每种特定数据类型及其二元操作对应一棵。第二种方法只使用一棵增强型B+树，该树具有与所有相关数据类型和二元操作组合相关的复杂结构。最佳方法的选择取决于应用，因为复杂解决方案的性能取决于最频繁操作的运行时间。

在简单的应用中，增强型B+树的每个特定变体都实现了计数子结构以获得高效的序列操作，并且只实现了一个特定于二元操作的子结构。它可以是用于快速求和的元素值和子结构，也可以是用于计算最小值或查找给定范围内最小元素的最小值子结构。以下代码演示了计算给定范围内容器元素值的和。

std::plus<int>     bop_add ;
bp_tree_bin_op< int, std::plus<int> >
                   semigroup ( bop_add ) ; 
// ... 
sum = semigroup . reduce ( iter_a , iter_b ) ;

泛化的优点是，使用成员函数 bp_tree_bin_op::reduce() 比使用“基本算法泛化”一节中考虑的算法 std::accumulate() 更简单。最小值的计算仅在二元操作类型上有所不同。

min_value<int>      bop_min ;
bp_tree_bin_op< int, min_value<int> >
                    semigroup ( bop_min ) ; 
// ... 
val_min = semigroup . reduce ( iter_a , iter_b ) ;

与聚合树的比较

B树和B+树是存储外部存储器中海量数据并对其进行高效操作的主要数据结构[2]。SQL提供了聚合函数，可用于快速计算统计参数：min, max, sum, count, avg。这些查询由聚合树支持，聚合树是增强型B+树的一种变体，类似于此处讨论的变体。对基于内部和外部存储器数据结构的算法进行简要比较，可以为高效算法的设计提供有用的见解。

在为外部搜索设计的B+树中，对象通过其键进行标识。为了获得最佳的范围搜索性能，此类B+树以其键的非递减顺序存储对象。就C++标准容器而言，用于外部搜索的B+树表示一个有序的std::multiset或std::set。这种类型的树并非设计用于支持无序容器。序列，例如std::vector，不限制容器中的元素必须有序。在序列中，元素通过其秩进行标识。本文讨论的增强型B+树通过计数子结构提供对秩的高效操作。

任何B+树都具有针对对所有元素进行顺序访问而优化的结构，通过连接最深层节点来实现。然而，在用于外部搜索的B+树中，内部层级的兄弟节点未链接。因此，这些B+树不支持前面讨论的最短路径算法。高效计算聚合B+树中存储数据统计参数的算法是从根开始并遍历B+树所有层级的自顶向下搜索[3]。

此处讨论的层级链接B+树也可以支持自顶向下算法，但对于此树来说，它并非渐近最优。自顶向下算法不如最短路径算法高效，尽管两种算法都保证对数性能。自顶向下算法遍历树的所有层级，因此其运行时间与树中元素总数呈对数关系。最短路径算法的运行时间与给定范围内元素数量呈对数关系，因为它只访问所需数量的低层树。

在二元运算泛化的背景下，自顶向下算法的直接实现不适用于半群的表示。树节点中存储数据的自顶向下处理顺序要求二元运算是可交换的而不是结合的。理论上，可以保证预计算数据的正确处理顺序，但这会使实现代码更复杂。实现还应解决最小值和最大值二元运算中具有无限值的单位元问题。

所提出的增强型B+树的高度通用性使其能够支持聚合树的功能。这是增强型B+树高级应用的一个例子。它也很好地说明了使用C++进行泛型编程的强大功能，它能够以高通用性和高效率低成本地开发复杂算法。

通过使用一个增强型B+树，可以同时计算多个统计参数，该树提供了计数子结构以及前面讨论的几种基本子结构的组合。该解决方案需要一个用户定义类型，用于收集应用程序特定的预计算数据并将其存储在树的节点中。在示例代码中，一个容器元素具有以下数据

template < class _Ty_Elem >
struct NodeData
{
    _Ty_Elem    sum ;   //  the sum of values of container elements
    _Ty_Elem    min ;   //  the minimum value of container elements  
    _Ty_Elem    max ;   //  the maximum value of container elements  
    // ...
} ;

这些数据的所有二元运算都在函数对象中组合，该函数对象用作 class bp_tree_bin_op 中相应模板参数的参数

template < class _Ty_Elem >
struct BinOperationNodeData 
{
    typedef NodeData<_Ty_Elem>  NodeDataElem ; 
    
    NodeDataElem  operator ( ) ( NodeDataElem const &  a , NodeDataElem const &  b ) const 
    {
        NodeDataElem    res ; 
        res.sum = ( a.sum + b.sum ) ;
        res.min = ( b.min < a.min ) ? b.min : a.min ;
        res.max = ( a.max < b.max ) ? b.max : a.max ;
        return res ; 
    } 
} ;

使用此用户定义类型和二元操作，一次调用函数

NodeData<T>
bp_tree_bin_op< NodeData<T>, BinOperationNodeData<T> >::reduce( const_iterator  pos_a ,
                                                                const_iterator  pos_b ) const ; 

返回连续元素的多个统计参数：值之和、最小值和最大值。获取所有这些值的运行时间与给定范围内元素的数量呈对数关系。

SemiGroupAddMinMax  semigroup ( bin_op_data ) ; 
// ...

IteratorND  iter_a = semigroup.begin() + dist_a ;
IteratorND  iter_b = semigroup.begin() + dist_b ;
int         count  = iter_b - iter_a ; 
data_reduce = semigroup . reduce ( iter_a , iter_b ) ; 

//  these results demonstrate facilities of aggregation trees 
cout << "semigroup.reduce()" << endl ;
cout << "with the facilities of aggregation trees:" << endl ;
cout << "  sum = " << data_reduce.sum << " ;" << std::endl ; 
cout << "  min = " << data_reduce.min << " ;" << std::endl ; 
cout << "  max = " << data_reduce.max << " ;" << std::endl ; 
cout << "  count   = " << count << " ;" << endl ; 
cout << "  average = " << double( data_reduce.sum ) / double( count ) << " ;" << endl ; 

演示代码展示了如何使用两个迭代器之间的差值来计算元素计数。这是一个非常高效的操作，具有常数时间复杂度。所得的总和除以计数即为范围内元素值的平均值。

对于实际应用，示例代码的空间效率可以优化。为了避免数据重复，外部节点只能存储容器元素，而不存储内部节点所需的任何其他类型的预计算数据。演示代码未涵盖标准差的快速计算，标准差是另一个重要的统计参数。此计算通过在内部节点中存储元素的平方值附加和来实现[1]。

性能

性能分析在应用中很重要，尽管它可能是一项艰巨的任务。算法的编程实现性能并不总是与提供渐近计算复杂度的抽象模型一致。在大多数现代计算机系统中，物理内存有几个缓存级别，访问数据的效率不同。测试算法的运行时间可能受到复杂的虚拟内存管理算法的影响。在模型中恒定的操作成本，在实践中通常是问题规模的函数。

为了了解C++中半群的有效表示有多大用处，测试了两个参数不同的系统

• Windows 7 专业版，64位；PC；处理器：Intel i7-3770，3.40GHz，核心数=4，线程数=8；RAM=24GB；缓存：L1=256KB，L2=1MB，L3=8MB。
• Android v. 4.1.2; 三星 Galaxy III, GT-19305T; 处理器: 四核 Cortex-A9, 1.4GHz; RAM=2GB; 缓存: L1=32 KB, L2=1 MB。

测试的主要目标是测量最短路径算法与标准顺序处理范围内所有元素相比提供的性能增益。预计计算的运行时间将从线性渐近地改进为对数。附件文件"semigroup_performance.hpp"中的测试函数以容器类型、其元素和二元操作为参数。这些测试可用于比较半群与标准序列容器的性能。对于容器元素，目前支持三种类型：int、double和complex<double>。如前所述，由于溢出错误，int类型不适用于实际应用。然而，这种类型有助于估计引用局部性效应和FPU的计算能力。每个测试算法都在for循环中运行。测试运行次数可以改变以控制精度。

为了更真实的场景，我们在这里考虑 double 类型值求和的性能。树最深层存储的值的总和已使用标准函数 std::accumulate() 计算。相同范围内值的快速求和使用函数 bp_tree_bin_op::reduce()。前两张表显示了运行时间（微秒）与范围内元素数量 (N) 的关系。性能增益测量为两个函数运行时间的比率。

第一张表显示了Windows系统的结果

N	500	5,000	50,000	500,000
累加()	0.73	7.2	73	1,620
减少()	0.064	0.080	0.11	0.140
增益	11.4	90	660	11,600

第二张表显示了Android系统的结果

N	500	5,000	50,000	500,000
累加()	36	400	4,100	42,000
减少()	3.55	4.65	5.90	7.29
增益	10.1	86	690	5,760

两个被测系统都显示出相当大的性能提升，随着范围内元素数量的增加而增加。总的来说，测量的运行时间与模型性能估算一致。在Windows系统上，当N=500,000时，std::accumulate()的偏差最为显著。运行时间的超线性增长（1,620mcs而不是预期的730mcs）通常是由缓存未命中的数量增加引起的。这一事实以及Windows系统上std::accumulate()的运行时间大约快50倍的事实表明，该系统利用了大型缓存。

这些测试中一个有趣且令人惊讶的发现是，尽管系统参数和测量运行时间存在显著差异，但两个系统的性能增益基本相同。这与500到50,000个元素范围内预期的N / log N增益一致。

N	500	5,000	50,000	500,000
Windows 增益	11.4	90	660	11,600
安卓增益	10.1	86	690	5,760

这些性能测试结果表明，C++中高效的半群不仅在测试系统中，而且在许多其他类型的计算机系统中都应该是有益的。

Using the Code

所附代码仅用于说明目的。

类模板bp_tree_bin_op（在文件"bp_tree_bin_op.hpp"中）表示增强型B+树的演示版本，可用于在C++中开发高效的半群。主接口成员函数bp_tree_bin_op::reduce()实现了一个顺序处理算法，该算法在给定范围内元素数量上具有对数运行时间，假设结合二元运算的成本是常数。

class bp_tree_bin_op是使用增强型B+树开发的，该树支持C++03标准容器的接口和快速求和算法，即项目STL Extensions中的class bp_tree_array_acc。增强型B+树的演示版本实现了前身的一小部分操作。class bp_tree_bin_op仅支持标准序列容器std::vector的有限功能。

文件"semigroup_demo.cpp"提供了本文讨论的基本和高级示例代码。

参考文献

1. V. Stadnik. 使用增强数据结构的快速顺序求和算法。arXiv:1404.1560, 2014. (http://arxiv.org/abs/1404.1560)

2. D. Comer. 无处不在的B树。ACM计算调查，11(2)，第121-137页，1979。

3. D. Zhang. B树。载于数据结构与应用手册，D. Mehta和S. Sahni（编），CRC出版社，2005。