音乐录音中的脉冲噪声检测和消除

下载 INDC.zip

引言

在收听存档的音乐唱片时，我们经常会遇到（或者更确切地说，听到）脉冲噪声出现的问——所谓的“噼啪声”。在收听黑胶唱片或磁带时，这个问题会更加严重。

有许多算法可以去除这类失真——有些适合硬件实现，有些只能用于离线实现。

本文旨在介绍指数加权最小二乘法 (EWLS) 识别方法和下一步误差预测分析的应用。

尽管该算法将用于检测和消除录制的音乐中的噪声，但它也可以成功地用于消除任何一组（甚至多维）信号中的脉冲噪声。

声学信号

我们现实世界中存在的声学信号是连续时间信号，并以这种形式记录在黑胶唱片或磁带等模拟介质上。

记录在更现代的数字数据介质（CD、硬盘、闪存）上需要对模拟信号进行数字化——采样和量化。

人耳听到的声音频率范围大约在 20 kHz 左右。根据奈奎斯特定理，为了避免混叠效应，采样频率应至少是信号频谱中最高频率峰值的两倍。在音乐处理中，我们使用了 44.1 kHz 的采样频率。

在本文中，我们将假设处理的信号是数字信号，并且已根据奈奎斯特定理正确采样。

信号估计

数字声学信号可以看作是一个离散时间函数f(t)，其中 t = 0, 1, … 表示归一化时间。假设下一个函数值（信号样本）可以用自回归模型 (AR) 表示

其中  表示时刻  的信号样本值， 表示时间移位算子， 表示 AR 模型的阶数， 表示第 i 个模型参数， 表示白噪声。

我们假设向量

和

使用它们，我们可以重新排列自回归模型方程

如果我们假设向量  表示  信号的真实（我们未知）参数，那么我们可以假设存在一个向量  ，它是向量  的估计。

递归识别算法根据收集到当前步骤为止的数据（值）来计算下一个信号值的预测  

 

递归识别算法

根据上述方程，如果我们想计算下一步的信号值预测，我们需要将向量 定义为向量  是先前操作的结果。

为了计算 ，我们将使用指数加权最小二乘法 (EWLS)。EWLS 算法，作为最小二乘算法家族中的一员，通过最小化最小二乘成本函数来计算模型参数——在 EWLS 中，它赋予先前误差值指数级的较低权重。

为了减小旧值对当前计算的影响，我们需要假设一个所谓的遗忘因子 。遗忘因子取值在 0 到 1 之间，其中如果  ，则 EWLS 算法的记忆更短。

递归 EWLS 由以下方程给出

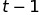其中  是误差函数——在  时刻的真实信号值与在  时刻的估计信号值之间的差值。

而  是一个增益向量，其描述如下：

其中矩阵  可以通过以下方程计算：

 

干扰检测

二维信号中的脉冲噪声可以看作是幅度远高于相邻样本的样本（图 1）。

图 1. 声学信号中的脉冲噪声示例

为了检测这些样本，我们将使用基于误差函数预测的算法，定义为：

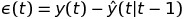
我们声明两个附加参数，第一个是预测误差的局部方差

第二个是预测误差的标准差

噪声检测是指验证  的值。自然，误差函数在  时刻的较高值表明该时刻的信号值受到干扰。

显然，上述条件非常模糊——“误差函数的较高值”是什么意思？

为了完善这个条件，我们假设声学信号的可疑样本会引起误差函数值大于该函数标准差的缩放值。

其中  是负责算法灵敏度的缩放系数，需要定义为算法的输入数据。请注意，过高的  值可能会导致遗漏受干扰的样本，而过低的值可能会导致将“干净”的样本分类为受干扰的样本。

用  表示一个二元函数，其可能值为 0（如果第 t 个样本是“干净”的）和 1（如果第 t 个值是受干扰的）。那么：

预测误差的局部方差可以使用以下公式计算：

初始条件为 。

 

损坏样本的重构

被标记为受干扰的样本将被删除并替换为重构的样本。为此，我们将使用相邻的“干净”样本进行线性插值。

另一个需要考虑的问题是可能受干扰的下一个样本的最大数量。因此，在下面的方程中应放置不同的  参数值：

其中 表示重构样本在步骤中的位置。

 

模拟

算法模拟中使用了初始参数。

对一段 20 秒的音乐记录进行了算法处理，结果如图 2 和图 3 所示。

图 2. 模拟结果。上图显示原始（受干扰）信号，下图显示检测和消除噪声后的信号。

图 3. 图 2 数据集的放大图。

 

代码使用

在 Matlab 环境中实现此算法非常容易，因为许多预定义函数都可以支持我们。

代码的使用方法是调用函数：

impulse_noise_elimination(file_1, file_2, model_order, n, lambda, p, save_ar)

其中

%Function Impulse Noise Elimination input parametres:
% * file_1 is a name of input track, ex. 'music.wav';
% * file_2 is a name of output track, ex. 'music_mod.wav';
% * model_order is a choosen number of estimated model parameters; can be
%   choosen from range: 1 <= model_order <= 25; mostly the best choice is
%   model_order = 4;
% * n is a scaling coefficient of local variance in detecting algorithm;
%   its value decides of the level of impulse noise samples; mostly n = 3
%   is the best choice, but n is from range 2 <= n <= 20;
% * lambda is a memory coefficient in EW - LS algorithm; its value
%   dependends on track dynamic; lambda is from the range: 
%   0.001 (low dynamic) <= lambda <= 0.999 (high dynamic);
% * p is a scaling coefficient of P matrix (eye matrix rank model_order)
%   starting value; p is from range 10^3 <= p <= 10^6;
% * save_ar = 0 or 1; 0 if model parametres should not be saved, 1 if model
%   parameters should be saved.

该函数的主要阶段如下所示。

输入数据检查

[track fs tmp] = wavread(file_1); %orginal track (wav file)

round(model_order);
round(n);

if model_order > 25
    model_order = 25;
elseif model_order < 1
    model_order = 1;
end

if n > 20
    n = 20;
elseif n < 2
    n = 1;
end

if lambda > 1
    lambda = 0.999;
elseif lambda < 0
    lambda = 0.001;
end

if p < 1000
    p = 1000;
elseif p > 1000000
    p = 1000000;
end

if save_ar ~= 1
    save_ar = 0;
elseif save_ar == 1
    model_vector = zeros(max(size(track)), model_order);
end

主循环步骤

初始参数

%Starting parametres of EW - LS algorithm:
org_track = track;
model = zeros(model_order, 1);
K = 0;
P = p * eye(model_order);
variance = 0;

循环定义

for t = (model_order + 1) : (max(size(track)) - 4)

% All operations

end

可以看到，循环的起始条件是：

(model_order + 1)

而结束条件是：

(max(size(track)) - 4)

因为我们需要收集至少模型阶数个样本才能开始识别，并且我们的实现考虑了接下来的四个样本可能受到干扰。

为了获取另一个信号值并计算预测误差，我们执行：

signal = track(t-1 : -1 : t-model_order);
prediction_error = track(t) - model' * signal;

当上一个样本是“干净”的时，可以计算方差。

variance = lambda*variance + (1 - lambda)*(prediction_error)^2;

否则，方差计算保持不变。为了初始化，我们使用：

variance = prediction_error^2;

检查接下来四个样本（当第一个样本受干扰时）最简单（非最优）的方法是使用 if 条件。

if abs(prediction_error) > n * sqrt(variance) %detecting test
    
    noise_samples = 1;
    signal_1 = track(t : -1 : t-model_order+1);
    prediction_error_1 = track(t+1) - model' * signal_1;

    if abs(prediction_error_1) > n * sqrt(variance)
        
        noise_samples = 2;
        signal_2 = track(t+1 : -1 : t-model_order+2);
        prediction_error_2 = track(t+2) - model' * signal_2;
        
        if abs(prediction_error_2) > n * sqrt(variance)
                        
            noise_samples = 3;
            signal_3 = track(t+2 : -1 : t-model_order+3);
            prediction_error_3 = track(t+3) - model' * signal_3;
            
            if abs(prediction_error_3) > n * sqrt(variance)
                
                noise_samples = 4;
                
            end
        end
    end

else
    noise_samples = 0;
    variance = lambda*variance + (1 - lambda)*(prediction_error)^2;
end

之后，我们可以尝试重构受干扰的样本。

if noise_samples ~= 0
    for i = 0 : noise_samples - 1
        track(t + i) = track(t-1) + (-1 / (noise_samples + 1))*(track(t-1) - track(t + noise_samples))*(i+1);
    end
    noise_samples = 0;
end

最后，我们可以更新我们的估计器参数。

prediction_error = track(t) - model' * signal;
K = (P * signal) / (lambda + signal'*P*signal);
P = (1 / lambda)*(P - (P*signal*signal'*P)/(lambda + signal'*P*signal));
model = model + K * prediction_error;

然后重新开始。

结论

提出的递归算法可以实现为实时应用。该算法产生的延迟取决于可能受干扰的下一个样本的最大数量。

本文所考虑的声学信号由于其幅度变化的动态性很高，因此这类信号可以使用此算法成功处理（例如测量数据）。

参考文献

[1] Niedźwiecki M. Kłaput T. Fast recursive basis function estimators for identification of time-varying processes., IEEE Transactions on signal processing, vol. 50, no. 8, pp. 1925 - 1934. August, 2002.

[2] Söderström T. Stoica P. System identyfication. Prentice-Hall International, Hemel Hempstead, 1989.

[3] Zieliński Tomasz P. Cyfrowe przetwarzanie sygnałów. Wydawnictwa Komunikacji i Łączności, Warszawa, 2005.