NURBS 曲线的简化
4.75/5 (34投票s)
NURBS 曲线的简化
注意
- 本文将向读者展示如何在不依赖任何现有NURBS库的情况下,绘制或设置NURBS曲线(无论是均匀还是非均匀)。
- 读者只需具备基本的OpenGL和freeglut绘图知识,能够绘制圆弧或圆形即可。
- 实际上,NURBS曲线既可以使用OpenGL绘制,也可以不使用OpenGL。这里之所以选择OpenGL,是因为作者将介绍一组新推导出的KNOTS-EQUATIONs(节点方程)作为核心算法,需要OpenGL函数进行验证。
NURBS与Bezier
NURBS广泛应用于计算机图形学和实体CAD应用程序中,许多程序员希望将其功能集成到自己的应用中,但网络上几乎没有**简洁**的开源库可用。因此,如果你想了解其内部原理,或许可以看看我对此的解读。
有些人可能认为NURBS很复杂,因为它有多种变体,如均匀/非均匀、有理/非有理。然而,如果你给我五到十分钟,我将向你展示NURBS和Bezier曲线一样简单。无论均匀或非均匀,NURBS本质上由一个或一组Bezier曲线构成;如果你愿意继续看下去,你只需要了解Bezier系列方程即可理解NURBS的数学原理。为了节省你记忆或查找常用Bezier方程的时间,我在下文图1中附上了它们。

NURBS的编程
在深入NURBS编程之前,我想再次强调,NURBS曲线实际上是一条或多条Bezier曲线首尾相连,并遵循特定数学约束规则。在微软的术语中,两条或多条连续连接的Bezier曲线称为Poly-Bezier。**因此,NURBS只是PolyBez的一个子集,其约束规则由节点数组(Knots-array)和NURBS基函数(NURBS Basis function)决定。**
稍后你会看到,节点数组是一组数字(整数或浮点数),它们除了控制点之外,也决定了NURBS的形状。**这意味着实际上有两个主要的变量控制NURBS的形状:一个是控制点,另一个是节点数组。** 然而,某些节点模式可能会导致特定的Bezier曲线段失效。因此,如果你想在你的代码中管理NURBS,首先需要一个工具来为复合Bezier曲线(polyBez)的每个段动态记录信息,我使用的是一个BitAry类。你可以自行在源代码中查看它,现在我们只需要了解为什么需要它。
接下来,我们需要为活动的NURBS准备三个数据数组用于**节点**,两个数据数组用于**控制点**,以及一个数据数组用于**polyBez控制点**。像我一样将它们准备好。
std::vector<Vec2D> CtrlPts; // core record of NURBS' control points std::vector<Vec2D> RingPts; // RingPts[], control-points used by Ring-NURBS. std::vector<double> coreNuts; // coreNuts is the base of Knots[] std::vector<double> OpenNuts; // knots array used by Open-NURBS std::vector<double> RingNuts; // knots array used by Ring-NURBS. std::vector<Vec2D> BezPts; // this is the polyBez array used to draw NURBS.
好的,你可能会问,我们要绘制多少个NURBS?为什么需要3个knots[] + 2个Ctrls[] + 1个BezPts[]?原因很简单,你需要一个节点数组作为核心基础;一个OpenNuts[]用于绘制NURBS的开放曲线,如果你想让曲线首尾相连形成一个**环**,则需要RingNuts[];OpenNuts[]和RingNuts[]都基于你的核心coreNuts[]。通过这种安排,你可以灵活地动态更改曲线形状所需的任何内容,并且你的程序将能够自由地沿着任何合理的NURBS路径绘制。
同样,对于两组控制点;第一个CtrlPts[]用于形成开放NURBS和你的核心控制点记录,第二个RingPts[]用于闭合的环形NURBS。
**哦,有一件重要的事情我忘了说,我们将通过PolyBez结构来绘制NURBS。** 这意味着我们必须能够首先将NURBS控制点转换为Bezier控制点。是的,你猜对了,这正是我们需要BezPts[]的原因。
为什么我们为一个NURBS需要这么多数组?
- 首先要了解的一个重要点是,当你改变节点的模式时,NURBS的形状也会随之改变。例如,如果进行裁剪(clamp),曲线可能会被约束在第一个或最后一个端点。如果程序需要改变裁剪状态,我实际上是将coreNuts[]复制到OpenNuts[],然后修改OpenNuts[]的第一个或最后几个元素来实现曲线的裁剪;一旦想取消裁剪,只需将coreNuts[]复制回OpenNuts[]即可。
 图2,coreNuts[] 与 OpenNuts[]
图2,coreNuts[] 与 OpenNuts[] - 第二件你需要理解的重要事情是,NURBS的**环形**实际上使用了比你从图中所见的更多的控制点。看看下面的NURBS,猜猜它用了多少控制点?


好的,在你准备好之后,我将开始向你展示一张关于**节点数组**和**控制点**之间关系的图。



**上述三幅图中的控制点与节点的关系**,可能是世界上首次展示,我不知道它们之前为什么没有出现在书籍或其他媒体中,无论如何,这是我的理解。
节点方程
**接下来,我将展示我的节点方程,它用于将NURBS转换为PolyBez,并且转换后的PolyBez仍然遵循NURBS的数学约束规则。** 你可能会问,为什么使用一些闻所未闻的方程?为什么不使用已有的方法?我想,除了我的方法,可能只有一种现有方法可以将NURBS转换回其PolyBez形式,那就是通过NURBS的基函数(Basis equations),你可以在维基百科上查阅。B-Spline或NURBS的**基函数方程**是一种递归算法,在我们的想象和编程中都是如此;由于是递归的,它比直接的函数稍慢。请看看我下面的方程,我相信你会发现我的方程更容易理解,并且比以往任何时候都更清晰地展示了CtrlPts[]和Knots[]之间的关系。




让我以三次NURBS为例来解释这些方程的用法,
- 首先,我们通常使用a、b、c、d来表示三次Bezier曲线的四个控制点,但在我的方程中,我使用v0、b0、c0和v1来表示Bezier段0的四个控制点,v1、b1、c1和v2表示段1,以此类推。
- 三次节点方程表明,变量bn和cn都依赖于NURBS控制点p0~pn;vn则是一个依赖于bn和c[n-1]的变量。由于vn的计算需要bn和c[n-1],因此当我们计划将三次NURBS转换为PolyBez形式时,所需的总Bezier控制点可以通过以下计算获得:
假设我们的目标三次NURBS有n个控制点;
那么它必须由(n-3)段三次Bezier曲线构成;
因此,所需的总Bez3控制点为(n-3)*3+1;
然而,我们需要c[-1]和b0来计算v0,以及c[n-1]和bn来计算vn,但cF(第一个c点)和bL(最后一个b点)并未计入(n-3)*3+1的计数中;
因此,转换所需的总临时Bez3控制点为(n-3)*3+3。
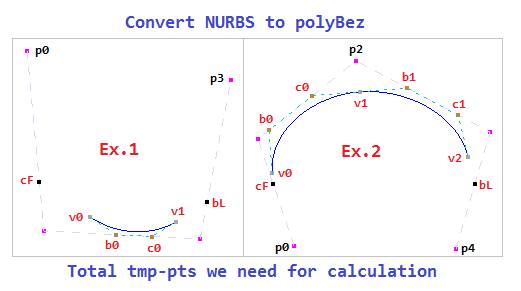 图 7
图 7 - 好了,请在这里稍加注意,这很重要。 你可以看到我的节点方程都在处理分数,并且每对bn和cn实际上共享相同的分母。那么,如果分母等于零怎么办?如果对于任何一对bn和cn出现这种情况,则意味着该对bn和cn无效或不存在;这意味着第n段的Bezier曲线也不存在。此外,变量vn也受相同的数学规则约束。
- 通过这些节点方程,你可以轻松地找到节点通过它们纠缠的关系对方向向量(即p[m] – p[n])产生的“作用力”分数。看看下面的方程,你就会明白我在说什么。
 图8,纠缠的节点。
图8,纠缠的节点。一旦你找到了由这些节点方程控制的数学关系,将其编码到你的程序中就只是一个简单的问题了。
现在你可以开始运行我的程序了,请先查看命令列表,了解你可以用它做什么,然后尝试单击鼠标并拖动你创建的点,看看程序的响应。但在深入体验之前,让我们回到正轨,完成NURBS的环形和有理部分。
环形NURBS的节点对齐
正如我之前提到的,形成一个**环**实际上需要比你从图中所见的更多的控制点。如果你忘了原因,请再次查看图4。我们选择将CtrlPts[]作为内核,而不是用RingPts[]替换它的原因在于,你的应用程序用户可以选择形成一个环,也可以选择将其再次断开。所以,正如我所提到的,NURBS由两个主要变量控制,一个是它的控制点,另一个是它的节点。现在是时候深入了解环形NURBS内部的节点是如何对齐的了。
在我看来,节点本身没有意义,真正的意义来自于我们在方程中找到的两个独立节点之间的差值。**虽然我们习惯称节点为“节点向量”(Knots-vector),但它实际上是一个标量,而不是向量;事实上,向量是由控制点(p[n+1] – p[n])构成的。** 因为只有控制点的坐标才能为我们提供空间方向,而节点与方向或方向变化完全无关。
那么,如何安排节点的变化来形成一个环?请看下面的图片。(我比较笨,总是画图来弄清楚我的问题是什么以及如何分析它;而且我猜你也发现了我在用英语描述事物之间的数学关系时有困难。)

有理NURBS
所谓的有理B样条(Rational-Bspline)与非有理B样条(Non-rational-Bspline)唯一的区别在于其每个控制点的权重因子。请快速浏览下面的图10,

你可以在图10中看到,以三次“**bn**”方程为例。在其有理方程中,除了控制点之外,都是标量,因此很容易通过改变一个表示权重因子的变量,使其再次看起来与非有理方程相似。此外,新的“**bn**”有理方程可以告诉我们,将非有理节点方程转换为有理节点方程不会改变其Bezier形式的控制点,唯一改变的是每个Bezier控制点的权重因子。这对我们来说是个好消息,无论你喜欢使用有理还是非有理形式的节点方程,从NURBS转换为BezPts[]的过程几乎都是相同的。

介绍结束
最后,这是关于如何构建不同形式NURBS曲线的介绍的结束。由于我的节点方程是将NURBS转换为poly-Bez形式的一种全新方法,也许有些人不相信我的数学可信度。请随意,我的源代码中有一个VERIFY命令,它使用OpenGL内置命令gluNurbsCurve()来绘制NURBS。你可以随时按“V”键来检查曲线,看看glu命令是否与我的代码绘制出相同的曲线?
同样,一旦你理解了我定义这些数据存储来处理不同形式NURBS的原因,阅读源代码本身就很容易了。所以,我让代码自己进行动态演示,否则你可能会对我的英语表达感到更加困惑。
我完全理解阅读我的文章不是一件令人兴奋的事情,但我仍然希望你能将我的源代码作为测试辅助工具来运行NURBS,如果你愿意,也可以将我的代码作为基础来开发你自己的NURBS类;你也可以通过设置自己的规则来生成非均匀节点,从而进一步简化它。但请注意,制定一个定义良好的节点对齐规则并非易事,祝你好运。
我希望这些方程、图片和我的代码能回答你关于NURBS曲线的所有问题。然而,如果你确实想直接问我问题,请使用简洁的英语,并请提前原谅我,如果我无法立即回答;因为我还在忙一些无法一直上网的事情。
3D进阶研究
我相信很多人有兴趣将NURBS应用于3D,并且不满足于只绘制2D曲线。在这种情况下,我建议你下载并研究由Rob Bateman先生编写的“Simple Bezier Patch Example”的源代码(请点击“OpenGL”菜单找到指定的示例代码)。我不认识他本人,但如果你想彻底理解NURBS曲面或Bezier Patch,那么我的节点方程加上他的代码示例可能是快速掌握的途径。
关于NURBS节点定义的疑难
- 节点是标量,不是向量。
- 节点重数(Multiplicity-of-Knots)的定义不正确。
我看到许多教科书做出了类似的定义,如下:
对于钳位B样条
第一个和最后一个节点值重复出现的重数等于阶(次数+1),这将使端点经过控制点。
对于三次B样条,第一个/最后一个节点的重数必须为4(重复四次)。
- 多余的节点。
例如,从我的节点方程中很容易发现,节点数组的**k0**和**kL**(最后一个元素)从未被使用,如果我没记错的话,这两个节点在B样条的基函数中也从未被使用。
描述
- 关于第二点,**创建首尾钳位的NURBS,重数仅为次数(degree),而不是阶(order)**(次数+1)。
例如,你可以自己测试节点模式k[] = {a,b,b,b,c,c,c,d} 配合三次4点NURBS,或者
k[] = {a,b,b,b,c,d,d,d,e} 配合三次5点NURBS。
并看看下面的示例图,
 图12,三次NURBS重数示例
图12,三次NURBS重数示例你也可以编写自己的代码,并使用原始OpenGL的gluNurbsCurve()命令来验证它们。
- 关于第三点,多余的节点,我不是第一个提出这个问题的人。你可以查看这个链接,了解McNeel-Wiki,它表达了相同的观点;我相信实现gluNurbsCurve()函数的程序员很久以前就知道这个问题了,因为它的很多行为都是正确的。我想这个问题之所以长期存在,只是因为直到我的方程出现之前,没有人能证明它是错误的。
总而言之,由于我不是训练有素的数学家(我甚至不知道如何正确写一篇数学论文),我认为最好将节点定义的问题留给专家们来解决。我只是尽力在这里展示我所学到的东西,并希望他们以后不再向年轻学生传授错误的信息。
gluNurbsCurve()的疑似bug
尽管我用它来验证我自行推导的节点方程的实现,但我发现这个命令有时无法正常工作。例如,你可以在自己的电脑上检查下面我收集的节点数据模式;因为我目前只在最旧版本的Microsoft内置opengl32.lib和glu32.lib上测试过它们。
1. k[]={0,3,5,9,9,9,9,9,11,13,15}; 8-points quadratic-NURBS;
2. k[]={0,3,3,3,3,5,9,9,9,9,9}; 7-points cubic-NURBS;
3. k[]={0,3,3,3,5,5,5,5,5,8,8,8,9}; 9-points cubic-NURBS;
4. k[]={0,3,3,3,5,5,5,5,5,5,8,8,8,9}; 10-points cubic-NURBS;
5. k[]={0,1,3,5,6,7,7,8,9,9,9,9,9,9,19}; 11-points cubic-NURBS;
6. k[]={0,1,2,3,3,3,3,3,3,3,5,8,8,8,9}; 10-points quartic-NURBS;
7. k[]={0,3,3,3,3,3,3,4,5,5,5,8,8,8,9}; 10-points quartic-NURBS;
gluNurbsCurve()命令无法为上述示例节点以及其他类似模式生成曲线。我不敢说这一定是OpenGL基础或Microsoft的bug,但我认为值得注意,因为我的方程可以为它们生成曲线。
顺便说一句,如果有人愿意检查我的节点方程,甚至对其进行某种形式的压力测试,我将非常欢迎。然而,如果有人想质疑我是否有资格提出这些关于数学定义或GL命令bug的问题,请先查看我过去的作品。
我知道我微不足道,所以我将把所有我开发出的信息留给你来评判。
更新于20150628
关于**节点数组是向量还是标量?**这个问题,我曾给密歇根理工大学的Ching-Kuang Shene教授写过邮件寻求指导,他告诉我:
“节点是有序标量,有序标量构成一个向量。‘节点向量’(knot vector)这个术语已经使用了三十多年,几乎所有NURBS的标准教科书都使用节点向量。”
因此,我在此更正我自己的误解是我的义务,非常感谢他对一个陌生人提供的友好回复。
