半素数有序序列（第 2 部分）

注意：本文的软件可从第一部分下载。

引言

本文解释了在无限模域上对半素数二元序列进行排序，是对《探索计算数论（第一部分）》的深入补充。与《探索计算数论（第一部分）》一样，本文在写作过程中参考了其他作者的素材，如下所示：

1. Mihnea Rădulescu 于 2011 年 9 月 23 日在 https://codeproject.org.cn/Articles/60108/BigInteger-Library 发表的《BigInteger 库》
2. Chew Keong TAN 于 2002 年 9 月 28 日在 https://codeproject.org.cn/Articles/2728/C-BigInteger-Class 发表的《C# BigInteger 类》
3. Adam Tibi 于 2013 年 6 月 13 日在 https://codeproject.org.cn/Articles/606446/UsingplusC-plus-NETplusUserplusDefinedplusFuncti 发表的《在 Excel 中使用 C# .NET 用户定义函数 (UDF)》
4. Excel-DNA 版本 0.32 可在此处获取 http://exceldna.codeplex.com/releases/view/119190。
5. Thomas Maierhofer (Tom) 于 2010 年 2 月 28 日在 https://codeproject.org.cn/Articles/61964/Performance-Tests-Precise-Run-Time-Measurements-wi 发表的《性能测试：使用 System.Diagnostics.Stopwatch 进行精确的运行时测量》

背景

在《探索计算数论（第一部分）》中，我曾讨论过一种非有序生成素数基序列的方法，换句话说，也就是半素数二元序列。本文介绍了一种同时生成和排序半素数二元序列的方法。半素数序列的研究需要大量的资源。下面的图表 1 展示了在排序过程的每个步骤中用于生成表格的时间资源，同时也是本文的目录。这些时间是在一台运行其他应用程序的笔记本电脑上生成的，并非在实时或优化的基准测试系统上。这只是一个一般性的时间参考，如果您决定重新生成表格，可能会遇到很大的时间差异。

计算

在本文中将使用以下数学关系，下面的图表 2 简要描述了这种关系，我将其称为“pMod iMod 表”。

1. pBase1 = 任何小于 pBase2 的素数
2. pBase2 = 任何大于 pBase1 的素数
3. N = pBase2 Mod pBase1
4. pMod = N – 1
5. iMod = (pBase1 Mod N) Mod pMod

请注意，上面的图表 2 中未用到素数 2 和 3。这些素数 {2, 3} 以及 iMod = 0 或 1 的素数对会产生平凡的余数，将在本文后面介绍。另请注意以下与最大公约数 (GCD) 的关系：

6. 如果 GCD(N, iMod) != 1，则素数对 {pBase1, pBase2} 不存在。

   示例：N = 10, pMod = 9，则对于 iMod = {2, 4, 5, 6, 8}，x = 不存在的对

图表 3 是“实际高低表”，是通过检查实际的二元序列生成的。

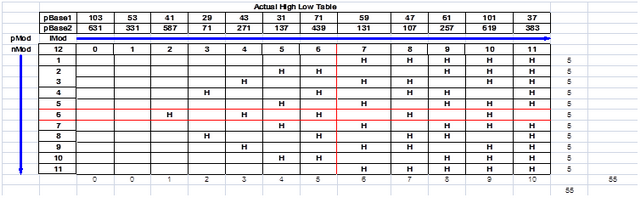
上面的图表 3 具有以下关系：

7. nMod = 一个大于 0 且小于 pMod 的数字，表示序列中 1 的残差增加（H 表示高位 = 1，空白表示低位 = 0）
   1. 如果 iMod = 0 或 1，则每个 iMod 的 ∑nMod = 0
   2. 如果 iMod > 1，则每个 iMod 的 ∑nMod = iMod – 1
8. ∑iMod = 每个 nMod 的 (pMod-2-x)/2
9. ∑∑iMod = ∑∑nMod = (pMod – 1) * (pMod – 1 – x)/2

象限

iMod = 2 -> pMod – 1（水平）	nMod = 1 -> pMod – 1（垂直）
第一象限左上角 = q1	第二象限右上角 = q2
第三象限左下角 = q3	第四象限右下角 = q4
pMod 为奇数时 iMod 边界 (pMod + 1)/2	pMod 为偶数时 iMod 边界在 pMod/2
nMod 边界在 (pMod - 1)/2	nMod 边界 pMod/2
iMod 边界永远不会是 H，因为 GCD(N, iMod) != 1	如果 iMod 为偶数，则 nMod 设置为 H
q1 [iMod, nMod] = - q2 [N - iMod, nMod]	q2 [iMod, nMod] = - q1 [N - iMod, nMod]
q1 [iMod, nMod] = q3 [iMod, pMod - nMod]	q2 [iMod, nMod] = - q3 [N - iMod, pMod - nMod]
q1 [iMod, nMod] = - q4 [N - iMod, pMod - nMod]	q2 [iMod, nMod] = q4 [iMod, pMod - nMod]
q3 [iMod, nMod] = q1 [iMod, pMod - nMod]	q4 [iMod, nMod] = - q1 [N - iMod, pMod - nMod]
q3 [iMod, nMod] = - q2 [N - iMod, pMod - nMod]	q4 [iMod, nMod] = q2 [iMod, pMod - nMod]
q3 [iMod, nMod] = - q4 [N - iMod, nMod]	q4 [iMod, nMod] = - q3 [N - iMod, nMod]

根据图表 4“第一象限高低表”及后续图表，可以得出以下关系：

10. nMod > 0 且 nMod < pMod，其中 nMod 为高位的数量等于 iMod – 1

    其中 iMod > 1。

    1. 如果 iMod 为偶数 && nMod = INT(pMod / 2)，则 nMod = 高位
    2. 如果 nMod 为偶数 && iMod = INT(pMod / 2)，则 nMod = 高位
    3. 如果 INT((1*pMod + 0) / iMod) = nMod，则 nMod = 高位
    4. 如果 INT((2*pMod + 1) / iMod) = nMod，则 nMod = 高位
    5. 如果 INT((3*pMod + 2) / iMod) = nMod，则 nMod = 高位
    6. 以此类推。

根据关系 10，可以创建“计算出的高低表”。见下面的图表 5。

错误检测

为了检查计算出的高低表中是否存在错误，可以对计算出的序列和实际序列进行比对检查。下面的图表 6 检查两个序列是否存在错误，并已手动修改以作为错误的示例。下面的图表 7 显示了检测到的错误对应的 pMod。

 

一旦知道了发生错误的 pMod（图表 7），就可以构建下面的图表 8 来指示序列中错误的精确位置。

下面的图表 9 显示了 pMod = 29 的简化算法展开过程。

算法展开过程

下面的图表 10 显示了 iMod < 2 的平凡余数的算法展开过程。

 

下面的图表 11 显示了 iMod > 1 的非平凡余数的简化算法展开过程。

时间成本

下面的图表 12 显示了在生成序列的同时对其进行排序所需的时间成本。可能会有人问：“为什么要对序列进行排序？”一个答案是：“它提供了一个研究半素数二元序列解构的工具。”

Using the Code

本项目构建为一个概念原型，因此不像更成熟的产品那样具有用户友好的错误检查功能。C# 代码是为 64 位系统构建的。Microsoft Office 2007 是一个 32 位环境，需要将 Excel-DNA 编译为 32 位。如果您希望此项目在 64 位版本的 Microsoft Office 上运行，则需要将 Excel-DNA 重新编译为 64 位。BigInteger 库已针对任意大小的整数进行了修改，并使用了 C# BigInteger 类中的例程来扩展支持本项目所需的算法。我还修改了 BigInteger 库，使其具有移位除法功能，以提高精度，但计算速度有所下降。BigInteger 库中还有其他几个支持例程，我已对其进行了修改，以提高精度或支持本项目。该代码应可用于 C# 项目、Excel VBA 和 Excel 电子表格中的实验。要在 Excel 中使用，请在电子表格中打开BigInteger-packed.xll，这将提供两个函数库：“BigInteger”和“Number Theory”。在 VBA 环境中引用BigInteger-packed.xll是某些宏生成本项目使用的电子表格或在其他 VBA 应用程序中使用所必需的。Microsoft Access 和 Excel 需要引用以下库：

1. Visual Basic For Applications
2. Microsoft Access 12.0 对象库
3. OLE Automation
4. Microsoft Office 12.0 Access 数据库引擎对象
5. Microsoft ActiveX Data Objects 6.1 库
6. BigIntExcel

如果您使用的是 .NET 4.0 或更高版本，您可能希望修改此项目代码以使用 Microsoft 的 Numeric 库。根据我的研究，除法算法是准确性和速度的关键。

关注点

由于“RegisterSize”函数会更改静态字段的值，因此此代码不是线程安全的。通过删除此函数，应可以相对直接地使本项目成为线程安全的。目前我尚未探索在多 CPU 环境中使用并行处理。Microsoft Excel 2007 中 BigInteger 的最大大小为 32,767 位十进制数字，如果超过此阈值，将导致计算错误。请参阅 https://support.office.com/en-us/article/Excel-specifications-and-limits-16c69c74-3d6a-4aaf-ba35-e6eb276e8eaa。

历史

这是该软件的第一个版本。