构建简单人工智能 .NET 库 - 第 6 部分 - 机器学习算法

• 下载 AI 库第 3 章 PDF - 1.5 MB

系列介绍

以下是本系列之前文章的链接

• 构建简单人工智能 .NET 库 - 第 1 部分 - 基础优先
• 构建简单人工智能 .NET 库 - 第 2 部分 - 机器学习入门
• 构建简单人工智能 .NET 库 - 第 3 部分 - 感知机
• 构建简单人工智能 .NET 库 - 第 4 部分 - 感知机与进阶
• 构建简单人工智能 .NET 库 - 第 5 部分 - 人工神经网络

我的目标是创建一个简单的人工智能库，涵盖一些高级人工智能主题，例如遗传算法、人工神经网络、模糊逻辑和其他进化算法。完成本系列的唯一挑战是是否有足够的时间来处理代码和文章。

代码本身可能不是主要目标，然而，理解这些算法才是。希望有一天它能对某人有所帮助。

请随时评论并提出任何澄清或希望提出的更好方法。

文章介绍 - 第 6 部分“机器学习算法”

我们在第二篇文章⁽²⁰⁾中讨论了机器学习（Machine Learning，ML）的类型（监督、无监督和强化）。这种分类主要基于“学习方法”。然而，这不足以定义“如何”进行学习的本质。

机器学习算法的另一种分类基于它们的功能，到目前为止，我们已经介绍了几种机器学习领域，如回归和分类。在本文中，我们将针对基于功能或所解决问题类型的 ML 算法。

请注意，为了简化和出于时间限制，将只展示算法、概念和最终公式，不提供统计学或数学证明。

什么是机器学习算法？

机器学习算法是用于从给定数据集中提取信息和/或检测模式的工具和技术。

我们为什么需要这些算法？显然，这应该满足人工智能作为概念的学习部分。

在下一节中，我们将介绍回归、分类和聚类。

1-回归算法

引用

回归⁽¹⁰⁾简单来说就是找到输入和输出（们）之间的最佳拟合映射（或关系）。

它代表了一个非常古老的统计学研究领域，有许多基于回归类型的分析方法。

回归分析是一种预测建模技术，它研究因变量（目标或标签）与自变量（输入或预测变量）之间的关系。该技术用于预测、时间序列建模以及寻找变量之间的因果效应关系。

回归分析是建模和分析数据的重要工具。在这里，我们对数据点拟合一条曲线/直线，使其与曲线或直线的数据点之间的距离差最小。

回归技术类型

一组变量之间的关系可以拟合不同的模型，最简单的是线性模型，其中直线可以是最佳拟合（在 2D 空间中）或平面（在 3D 空间中）或更高维空间中的超平面。

线性回归（2D）

非线性回归（2D）

线性回归（3D）

最流行的回归算法是

• 线性回归
• 逻辑回归
• 普通最小二乘回归（OLSR）
• 逐步回归
• 多元自适应回归样条（MARS）
• 局部散点平滑估计（LOESS）

2. 分类

分类也是一个映射函数，介于 X 输入和输出 Y 之间。其中 Y 是可能的类别。

如果回归是找到输入和输出之间的最佳拟合线，那么分类就是找到最佳区分线，将输入分离到一个或多个类别。

如果类别数量为两个，则称为二元分类。

如果有多个类别，则称为多类别分类。

与回归一样，它提供基于训练数据集的预测手段，因此分类属于监督式机器学习方法。

分类算法示例

• 线性分类器
• 逻辑回归
• 朴素贝叶斯分类器
• 感知器
• 支持向量机
• 二次分类器
• k-近邻
• 决策树
• 神经网络
• 学习向量量化

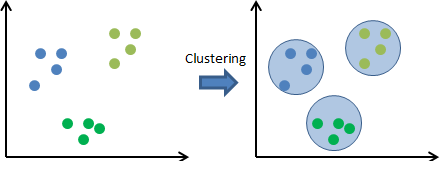
3. 聚类

聚类是分组（类似于分类），但没有预定义的标签（没有类别）。显然，它是无监督式机器学习算法的一部分。

要在没有预定义类别的情况下将对象分组，一种方法是根据距离或特征进行分组。实际上，不同的聚类算法使用不同的方法。

在上图所示，对象（输入）可以根据距离或其他特征集内的信息分为 3 组。

基于相似性的聚类有三种类型

I. 互斥聚类

一个对象只属于一个组

II. 重叠聚类

每个对象可以属于一个或多个组（簇）

III. 分层聚类

它更像树状关系。两个或多个簇可能具有父簇。

聚类算法类型

对象分组可以基于给定输入上的不同相似度量。以下是最常见的相似度量

连通性模型⁽²¹⁾

又名分层聚类，方法很简单；对象比距离较远的对象更接近于近对象。

质心模型⁽²²⁾

又名 K-Means 聚类算法，它是一种流行的算法，需要预先指定最终所需的簇数，这使得了解数据集的先验知识变得重要。这些模型通过迭代运行来找到局部最优解。

对象根据与簇质心的距离进行分组（聚类）。

分布模型

这些聚类模型基于一个想法，即一个簇中的所有数据点属于同一分布（例如：正态分布、高斯分布）的可能性有多大。这些模型的一个流行示例是期望最大化算法，该算法使用多元正态分布。

密度模型

这些模型搜索数据空间中数据点密度不同的区域。它分离出各种不同的密度区域，并将这些区域内的数据点分配到同一个簇。密度模型的流行示例是 DBSCAN 和 OPTICS。

以下是机器学习类型摘要

常见机器学习算法

1- 线性回归

线性回归，其中直线（或平面或超平面）可以是数据集之间的最佳拟合映射。

数据集是不同输入数据及其关联标签（实际输出）的样本，在这种情况下，输入称为自变量，输出称为因变量。

如果我们只有一个自变量（输入），则称为简单线性回归，但在有多个自变量的情况下，则称为多元线性回归。

线性回归参数

要理解线性回归，我们必须参考数学表示。因此，对于 2D 映射（变量之间的关系）和简单线性回归，我们将因变量表示为 Y，自变量表示为 X。为了使 Y 和 X 具有线性映射，我们需要找出直线方程，该方程可以实现这种线性。换句话说，Y & X 之间的映射应类似于

Y = a + m * X

其中

• a 是截距点（Y = 0 处的点），称为偏置系数
• m 是斜率（Y 变化量与 X 变化量的比率），称为系数

在 Y 依赖于多个输入的多元线性回归中，假设 X1, X2,……. Xn，方程应为

Y = a + m1 * X1 + m2 * X2+ . . . . . . . . + mn * Xn

因此，参数是 a 和 m（m1, m2, …. mn）。线性算法训练是指找到 a 和 m 的值，这些值可以提供最佳拟合方程。

有不同的训练算法可用于解决线性回归的参数，最常见的有

2- 简单线性回归

Y = a + m * X

假设从任何随机参数值开始，然后在数据集中给定样本 i，其中我们有对应于 Xi 的 Yi，我们可以定义该样本的误差为 Ei，其中

Ei = Yi – (估计输出)

Ei = Yi – (a + m * Xi)

将此误差平方为 (Ei)^2 = (Yi – (a + m * Xi))^2

通过对所有样本中的所有误差求和

为了找到可以最小化 SE（平方误差）的 a 和 m 的值，对 a 和 m 取导数，设置为 0，然后求解 a 和 m。由于简化和时间考虑，对数学公式的解释超出了本文的范围。最后，a 和 m 的最小二乘估计为

进一步，样本方差⁽¹¹⁾和样本协方差⁽¹²⁾定义为

因此，m 的方程可以简化为

1-   Calculate Average of inputs and Labels (Xavg & Yavg)
2-   Calculate sample Covariance
3-   Calculate sample Variance
4-   Calculate m = Cov/Var
5-   Calculate a= Yavg – m * Xavg

逻辑

创建了 SimpleRegression 类

Public Class SimpleRegression
    ''' <summary>
    ''' 1-       Calculate Average of inputs and Labels (Xavg and Yavg)
    '''     Average = sum/number
    ''' 2-       Calculate sample Covariance
    ''' 3-       Calculate sample Variance
    ''' 4-       Calculate m = Cov/Var
    ''' 5-       Calculate a= Yavg – m * Xavg
    ''' </summary>
    ''' <param name="X_Inputs"></param>
    ''' <param name="Y_Labels"></param>
    ''' <returns>Line with X as intercept and Y as slope</returns>
    Public Shared Function LineBestFit(X_Inputs As Matrix1D, Y_Labels As Matrix1D) As Vector
        Dim Line As New Vector
        Dim X_avg As Double = 0
        Dim Y_Avg As Double = 0
        Dim Cov_XY As Double = 0
        Dim Var_X As Double = 0
        Dim X_Copy As New Matrix1D(X_Inputs)
        Dim Y_Copy As New Matrix1D(Y_Labels)
        ' 1-     Calculate Average of inputs and Labels (Xavg & Yavg)
        X_avg = X_Inputs.Sum / X_Inputs.Size
        Y_Avg = Y_Labels.Sum / Y_Labels.Size
        ' 2-     Calculate sample Covariance
        X_Copy = X_Inputs.Sub(X_avg)
        Y_Copy = Y_Labels.Sub(Y_Avg)
        Cov_XY = X_Copy.Product(X_Copy, Y_Copy).Sum
        ' 3-     Calculate sample Variance
        Var_X = X_Copy.SquaredSum
        ' 4-     Calculate m = Cov/Var
        Line.y = CSng(Cov_XY / Var_X)
        ' 5-     Calculate a= Yavg – m * Xavg
        Line.x = CSng(Y_Avg - Line.y * X_avg)
        Return Line
    End Function
    
    ''' <summary>
    ''' Return MSE (Mean Square Error) from given Input Data set, 
    ''' Labels and estimated equation
    ''' </summary>
    ''' <param name="X_Inputs"></param>
    ''' <param name="Y_Labels"></param>
    ''' <param name="Line">X is intercept and Y is slope</param>
    ''' <returns></returns>
    Public Shared Function Validate(X_Inputs As Matrix1D, _
                  Y_Labels As Matrix1D, Line As Vector) As Single
        Dim Err As New Matrix1D(Y_Labels)
        Dim Y_Estimate As New Matrix1D(Y_Labels)
        Y_Estimate = X_Inputs.Product(Line.y)
        Y_Estimate = Y_Estimate.Add(Line.x)
        Err = Y_Labels.Sub(Y_Estimate)
        Return Err.SquaredSum / (2 * X_Inputs.Size)
    End Function
    
End Class

类包含函数 LineBestFit 和 Validate

• LineBestFit - 提供 a 和 m 的最佳拟合值
• Validate - 计算 MSE（均方误差）作为算法（最佳拟合）质量的度量

为了测试算法，创建了一个简单的窗体

算法评估

为了评估算法的准确性，计算 MSE（均方误差），但在某些参考文献中，也可能使用另一个参数，即回归标准误差或残差标准误差，表示为 s，其中：

3- 普通最小二乘法（OLS）

概念非常简单和合乎逻辑，将误差表示为实际标签（正确答案）和估计输出（基于初始直线方程）之间的距离，然后，该方法将数据集中所有样本的所有误差平方并求和，得到与简单回归相同的平方误差和，但适用于多个变量。

线性代数用于解决此模型⁽¹³⁾

4- 线性回归中的梯度下降

梯度下降用于找到函数的局部最小值，伪代码很简单

''' <summary>
''' Linear Regression Pseudo Algorithm to resolve h(x) = a + b * x
'''       1- Start with random values for a and b
'''       2- Iterate through given training set, for each:
'''            - Calculate h(x)
'''            - Calculate error = h(x) - Y where y is the correct answer or label
'''       3- Sum all errors
'''       4- Calculate MSE (Mean Squared Error) = 1/2*training set size * sum of all errors
'''       5- Get slope of line touching curve at the current point (for each value of a and b)
'''            - If +ve slope, move to left or Decrease a or b values
'''            - If -ve slope, move to right or increase a or b values
'''       6- Repeat above steps from 2 to 5 till direction or slope of calculated line changes
'''       7- Last values for a and b are the optimal values as per MSE minimization
''' </summary>

梯度下降已在文章 2⁽¹⁴⁾中解释

梯度下降

GD 使用上述伪代码最小化损失函数或成本函数，但它并不那么简单，尤其对于非线性函数。以下是一些 GD 方法

函数通常有一个全局最小值，但也可能有多个局部最小值，GD 可能会陷入其中一个局部最小值。

有许多类型的梯度下降算法，基于数据摄入

全批量 GD	一次使用全部数据计算梯度
随机 GD	从数据集中抽取一个样本来计算梯度

基于微分技术

一阶微分 GD	对成本函数使用一阶微分
二阶微分 GD	对成本函数使用二阶微分

梯度下降算法的变体（这里是 GD 方法的一个好参考）

• 标准梯度下降
• 动量
• Nesterov 加速梯度
• Adagrad
• Adadelta
• RMSprop
• Adam
• AdaMax
• Nadam

以下是一些方法。

I. 标准梯度下降

这是最简单的梯度下降技术形式。标准意味着纯粹的形式，没有任何掺杂。其主要特点是，我们通过计算成本函数的梯度，朝着最小值方向迈出小步。

Parameter_Update = learning_rate * gradient_of_parameters
Parameter_New_Value = Parameter_Old_Value - Update

学习率是一个非常重要的参数，在选择其值时应谨慎。

II. 带动量的 GD

在这里，我们通过一种方式调整上述算法，即在采取下一步之前，我们会考虑到上一步。

Parameter_Update = learning_rate * gradient_of_parameters
Velocity = Previous_update * momentum
Parameter_New_Value = Parameter_New_Value + Velocity – Parameter_Update

这里的更新与标准梯度下降相同。然而，增加了一个称为速度的新项，它考虑了先前的更新和一个称为动量的常数。

III. 自适应子梯度（AdaGrad）

ADAGRAD 使用自适应技术来改变学习率。它允许不同特征使用不同的步长。通常与随机 GD 一起使用。

Grad_component = Previous_grad_component + (gradient * gradient)
Rate_change = Square_root(grad_component) + epsilon
Adapted_learning_rate = learning_rate * rate_change
Parameter_update = Adapted_learning_rate * gradient
Parameter_New_Value = Parameter_Old_Value – Parameter_update

在上面的代码中，epsilon 是一个常数，用于控制学习率的变化速率。

IV. ADAM

ADAM 是另一种自适应技术，它建立在 adagrad 的基础上，并进一步减小了其缺点。换句话说，您可以将此视为动量 + ADAGRAD。

以下是伪代码。

Adapted_gradient = Previous_gradient + ((gradient – previous_gradient) * (1 – beta1))
Gradient_component = (gradient_change – previous_learning_rate)
Adapted_learning_rate =  previous_learning_rate + (gradient_component * (1 – beta2))
Parameter_Update = adapted_learning_rate * adapted_gradient
Parameter_New_Value = Parameter_Old_Value – Parameter_Update

这里的 beta1 和 beta2 是常数，用于控制梯度和学习率的变化。

5- 贝叶斯线性回归

贝叶斯线性回归是一种线性回归方法，其中统计分析在贝叶斯推断的背景下进行。当回归模型存在正态分布误差，并且假设了特定形式的先验分布时，可以得到模型参数后验概率分布的显式结果。

6- 多项式回归

多项式回归是一种回归分析形式，其中自变量 x 和因变量 y 之间的关系被建模为 x 的 n 次多项式。

n 次多项式可以表示为

多项式回归模型

这可以通过线性代数方法（矩阵转换）来解决。

使用普通最小二乘估计，可以解决为

虽然使用更高次多项式可以获得更低的误差，但如果验证不当，也可能导致过拟合。

7- 逐步回归

当处理多个自变量 X 时，使用此形式的回归。在此技术中，自变量的选择是通过自动过程完成的，该过程无需人工干预。

此建模技术的目标是使用最少的预测变量来最大化预测能力。它是处理数据集高维性的一种方法。

有关此算法的进一步信息（17），请参阅附件中的PDF 文档。

8- 正则化

正则化是一种最小化平方误差之和并降低模型复杂度以克服模型过拟合的技术。为了解释正则化，让我们探讨“过拟合”和“欠拟合”这两个术语。

过拟合

这是当模型描述随机误差或噪声而不是底层关系时。通常，这是当模型过于复杂时，例如参数数量相对于观测数量过多。

过拟合的模型预测性能较差，因为它对训练数据中的微小波动反应过度。

绿线代表过拟合模型，黑线代表正则化模型。虽然绿线最能拟合训练数据，但它过度依赖于训练数据，并且在新的未见数据上可能具有更高的误差率，与黑线相比（16）。

欠拟合

当模型或机器学习算法无法捕捉数据的潜在趋势时，就会发生欠拟合。例如，当将线性模型拟合到非线性数据时，就会发生欠拟合。这样的模型预测性能会很差。

线性回归的两种流行正则化过程示例是

• Lasso 回归：将普通最小二乘法修改为也最小化系数的绝对和（称为 L1 正则化）。
• Ridge 回归：将普通最小二乘法修改为也最小化系数的平方绝对和（称为 L2 正则化）。

当输入值存在共线性且普通最小二乘法会过拟合训练数据时，使用这些方法很有效。

9- Ridge 回归

Ridge 回归是一种在数据存在多重共线性（自变量高度相关）时使用的技术。在多重共线性中，即使最小二乘估计（OLS）无偏；但它们的方差很大，导致观测值与真实值偏离较大。通过在回归估计中增加一定程度的偏差，Ridge 回归可以减小标准误差。

对于平方误差和 SSE

Yi 是标签或正确答案。

F(x) 是预测值或猜测值 = Y。

Ridge 回归执行“L2 正则化”，即在优化目标中添加了系数平方和的因子。因此，我们需要向方程引入一个额外的项

目标 = 残差平方和 + lambda * (系数平方和)

这里的 lambda 是一个从模型外部确定的收缩因子（它是一个调优参数），它为我们希望惩罚系数平方和的程度分配一个权重。

这里，lambda 是一个参数，它平衡了最小化 RSS 和最小化系数平方和之间的侧重点。lambda 可以取各种值

lambda = 0

目标与简单线性回归相同。

lambda = ∞

系数将为零。为什么？因为平方系数具有无限权重，任何小于零的值都会使目标值无穷大。

0 < lambda < ∞

lambda 的大小将决定对目标不同部分赋予的权重。

对于简单线性回归，系数将在 0 和 1 之间。

任何非零值将给出小于简单线性回归的值。

随着 alpha 值的增加，模型复杂度会降低。

10- Lasso 回归

LASSO 代表最小绝对收缩和选择算子。

Lasso 回归执行L1 正则化，即在优化目标中添加了系数绝对值之和的因子。因此，lasso 回归优化以下内容

目标 = SSE + lambda * (系数绝对值之和)

这里，lambda 的作用与 ridge 类似，提供了 SSE 和系数大小之间的权衡。与 ridge 类似，lambda 可以取各种值

lambda = 0：系数与简单线性回归相同

lambda = ∞：所有系数为零（逻辑同上）

0 < lambda < ∞：系数介于 0 和简单线性回归的系数之间

11- Logistic 回归

这项机器学习技术通常用于二元分类问题，即存在两种可能的结果（是或否），这些结果受一个或多个解释变量的影响。该算法根据一组观测变量估计结果的概率。

Logistic 回归属于一类称为广义线性模型（GLM）的算法。

Logistic 回归可以简单地理解为找到最佳拟合的 Beta 参数

使用的假设函数是 Logistic 形式。

在这种情况下，t 为

在矩阵形式下

因此，h(x) 可以写成

GD 可用于解决 Beta（权重）值。伪代码可以简化为

For Single Classifier (one discrete output):

Initialize Random Weights
Initialize Learning_rate
Iterate from i=1 to m (m is number of samples in data set)
   Calculate Sum_Of_Errors
   Err(i) = h(x(i)) – Label(i)
   Scale Err to Input Err=Err(i) * X(i)
   Sum = Sum + Err(i)
End loop
Weight_New_Value = Weight_old_value - Sum * Learning_rate

上述代码用于单个分类器，对于多分类器，n 个类别

For Multi-Classes Classifiers:

Initialize Random Weights
Initialize Learning_rate
Iterate for all classes j = 1 to n (n is number of classes)
   Sum = 0
   Iterate from i=1 to m (m is number of samples in data set)
      Calculate Sum_Of_Errors
      Err(i) = h(x(i)) – Label(i)
      Scale Err to Input Err=Err(i) * X(i)(j)
      Sum = Sum + Err(i)
   End Loop
Weight_New_Value(j) = Weight_old_value(j) - Sum * Learning_rate
End loop

12- K-means 聚类

该算法旨在解决聚类问题，即您拥有输入（特征）的数据集，但没有标签（正确答案）。因此，这是一种无监督学习算法。

K-Means 聚类接收 n 个特征并将其分类为 k 个类。但是，如何确定一个输入（特征）属于 A 类还是 B 类？该算法使用欧几里得距离 ⁽¹⁸⁾作为分类器。简单来说，如果一个点离 A 类的中心点更近，则它属于 A 类，否则。

以下是具有 2D（2 个特征）和 3D（3 个特征）的 K-Means 聚类

K-Means 聚类伪代码

Get Data set of n features and k classes
Initialize random k means (known as centroids) m1,m2, …… , mk
Loop until there is no more moves Euclidean distance and classify all points
    Based on random means, calculate
    For i = 1 to k
        Replace mi with the mean of all of the samples for cluster i
    End For
End Loop

13- K 最近邻 - 分类

K 最近邻是一个简单的算法，它存储所有可用的案例，并根据相似度量（距离函数）对新案例进行分类。K 是要考虑的邻居数量。

算法

一个点通过其邻居（k）的多数投票进行分类，该点被分配到其 K 个最近邻中通过距离函数测量的最常见的类别。如果 K = 1，则该点简单地分配给其最近邻的类别。

关注点

本文是常见机器学习算法的摘要，它既不完整也不详尽的摘要，因为有大量的算法。仅专注于常见的类型。

本文可能还有第二部分。

本文顶部附有本文的 PDF 版本。

参考文献

• (20) https://codeproject.org.cn/Articles/1205296/Build-Simple-AI-NET-Library-Part-Machine-Learnin
• (21) https://en.wikipedia.org/wiki/Hierarchical_clustering
• (22) https://en.wikipedia.org/wiki/K-means_clustering

历史

• 2017 年 9 月 29 日：初始版本