使用 Python+Keras 进行基础深度学习。第 2 章
3.93/5 (5投票s)
这是介绍 Python 和 Keras 框架中深度学习编码的文章系列的第二篇文章。
引言
本文不为您介绍深度学习。您应该了解深度学习的基础知识和一些 Python 编程。本文的主要目的是向您介绍 Keras 框架的基础知识,并与另一个知名库一起进行快速实验,得出初步结论。
背景
在上一篇文章中,我们训练了一个简单的神经网络。这次,我们将训练一个卷积神经网络,并与之前的结果进行比较。

所有实验均出于教学目的,训练过程将非常快速,结果也不会完美。
Using the Code
我们想训练一个简单的卷积神经网络。在以下链接中,您可以了解卷积网络与常规或传统神经网络的对比介绍。
Keras 提供了轻松构建卷积神经网络的所有工具。用于查看模型质量的所有工具与我们在上一篇文章中使用的工具相同。
第一步:加载库
与上一篇文章一样,我们需要加载所有需要的库:numpy、TensorFlow、Keras、Scikit Learn、Pandas……以及更多。
import numpy as np
from scipy import misc
from PIL import Image
import glob
import matplotlib.pyplot as plt
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline
from IPython.display import SVG
import cv2
import seaborn as sn
import pandas as pd
import pickle
from keras import layers
from keras.layers import Flatten, Input, Add, Dense, Activation, ZeroPadding2D,
BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D, Dropout
from keras.models import Sequential, Model, load_model
from keras.preprocessing import image
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.applications.imagenet_utils import decode_predictions
from keras.utils import layer_utils, np_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from keras.initializers import glorot_uniform
from keras import losses
import keras.backend as K
from keras.callbacks import ModelCheckpoint
from sklearn.metrics import confusion_matrix, classification_report
import tensorflow as tf
设置数据集
我们使用CIFAR-100 数据集。该数据集已使用很长时间。它每个类别有 600 张图像,共 100 个类别。每个类别的训练集有 500 张图像,验证集有 100 张图像。100 个类别中的每一个都分为 20 个超类。每张图像都有一个“精细”标签(主要类别)和一个“粗略”标签(其超类)。
Keras 框架提供了直接下载的模块
from keras.datasets import cifar100
(x_train_original, y_train_original),
(x_test_original, y_test_original) = cifar100.load_data(label_mode='fine')
实际上,我们已经下载了训练集和测试集。x_train_original 和 x_test_original 分别包含训练和测试图像,而 y_train_original 和 y_test_original 包含标签。
让我们看看 y_train_original
array([[19], [29], [ 0], ..., [ 3], [ 7], [73]])
如您所见,这是一个数组,其中每个数字对应一个标签。因此,我们要做的第一件事是将这些数组转换为独热编码版本(请参阅维基百科)。
y_train = np_utils.to_categorical(y_train_original, 100)
y_test = np_utils.to_categorical(y_test_original, 100)
好的,现在让我们看看训练集(x_train_original)
array([[[255, 255, 255],
[255, 255, 255],
[255, 255, 255],
...,
[195, 205, 193],
[212, 224, 204],
[182, 194, 167]],
[[255, 255, 255],
[254, 254, 254],
[254, 254, 254],
...,
[170, 176, 150],
[161, 168, 130],
[146, 154, 113]],
[[255, 255, 255],
[254, 254, 254],
[255, 255, 255],
...,
[189, 199, 169],
[166, 178, 130],
[121, 133, 87]],
...,
[[148, 185, 79],
[142, 182, 57],
[140, 179, 60],
...,
[ 30, 17, 1],
[ 65, 62, 15],
[ 76, 77, 20]],
[[122, 157, 66],
[120, 155, 58],
[126, 160, 71],
...,
[ 22, 16, 3],
[ 97, 112, 56],
[141, 161, 87]],
...and more...
], dtype=uint8)
该数据集代表 256 个 RGB 像素的 3 个通道。想看看吗?
imgplot = plt.imshow(x_train_original[3]) plt.show()

接下来,我们需要对图像进行归一化。也就是说,将 dataset 中的每个元素除以总像素数:255。完成后,数组的值将在 0 到 1 之间。
x_train = x_train_original/255
x_test = x_test_original/255
设置训练环境
在训练之前,我们必须在 Keras 环境中设置两个参数。首先,我们必须告诉 Keras 通道在数组中的哪个位置。在图像数组中,通道可以位于最后一个索引或第一个索引。这被称为通道优先(channels first)或通道后(channels last)。在我们的练习中,我们将设置为通道后。
K.set_image_data_format('channels_last')
第二件事是告知 Keras 当前处于什么阶段。在我们的情况下,是学习阶段。
K.set_learning_phase(1)
在接下来的文章中,我们将不再展示这两个部分,因为它们在所有文章中都是相同的。
训练卷积神经网络
在此步骤中,我们将定义 ConvNet 模型。
def create_simple_cnn():
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), input_shape=(32, 32, 3), activation='relu'))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(256, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(512, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(1024, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(500, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(100, activation='softmax'))
return model
如您在代码中所见,Conv2D 行引入了一个卷积层,而 **MaxPooling 行** 引入了池化层(在此网络中,我们使用了 **最大池化**,但我们也可以使用 **平均池化**)。对于每个卷积层,我们使用 ReLu 激活函数。另一个重要指令是 **Dropout**,通过它,我们进行小的正则化。
模型定义后,我们进行编译,设置优化函数、损失函数和指标。与之前的实验一样,我们使用 **随机梯度下降**、**分类交叉熵**,以及指标 **准确率** 和 **mse**(均方误差)。
scnn_model = create_simple_cnn()
scnn_model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['acc', 'mse'])
好的,让我们看看这个模型的摘要。
scnn_model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_7 (Conv2D) (None, 30, 30, 32) 896
_________________________________________________________________
conv2d_8 (Conv2D) (None, 28, 28, 64) 18496
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 14, 14, 64) 0
_________________________________________________________________
conv2d_9 (Conv2D) (None, 12, 12, 128) 73856
_________________________________________________________________
conv2d_10 (Conv2D) (None, 10, 10, 256) 295168
_________________________________________________________________
conv2d_11 (Conv2D) (None, 8, 8, 512) 1180160
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 4, 4, 512) 0
_________________________________________________________________
conv2d_12 (Conv2D) (None, 2, 2, 1024) 4719616
_________________________________________________________________
max_pooling2d_6 (MaxPooling2 (None, 1, 1, 1024) 0
_________________________________________________________________
flatten_2 (Flatten) (None, 1024) 0
_________________________________________________________________
dense_3 (Dense) (None, 500) 512500
_________________________________________________________________
dropout_4 (Dropout) (None, 500) 0
_________________________________________________________________
dense_4 (Dense) (None, 100) 50100
=================================================================
Total params: 6,850,792
Trainable params: 6,850,792
Non-trainable params: 0
_________________________________________________________________
我们可以看到参数数量翻了一番。尽管参数数量翻倍,但如果我们能使用一个常规网络,实际参数数量应该会更高。通过卷积步骤,网络将提取图像的特征。
那么,下一步就是训练模型。
scnn = scnn_model.fit(x=x_train, y=y_train, batch_size=32, epochs=10,
verbose=1, validation_data=(x_test, y_test), shuffle=True)
我们将以与上次实验相同的方式训练此模型。我们将使用批量大小为 32(以减少内存占用)并进行 10 个 epoch。结果存储在 scnn 变量中。如您所见,指令是相同的。
Train on 50000 samples, validate on 10000 samples
Epoch 1/10
50000/50000 [==============================] - 59s 1ms/step - loss: 4.5980
- acc: 0.0136 - mean_squared_error: 0.0099 - val_loss: 4.5637 - val_acc: 0.0233
- val_mean_squared_error: 0.0099
Epoch 2/10
50000/50000 [==============================] - 58s 1ms/step - loss: 4.4183
- acc: 0.0302 - mean_squared_error: 0.0099 - val_loss: 4.3002 - val_acc: 0.0372
- val_mean_squared_error: 0.0098
Epoch 3/10
50000/50000 [==============================] - 58s 1ms/step - loss: 4.2146
- acc: 0.0549 - mean_squared_error: 0.0098 - val_loss: 4.1151 - val_acc: 0.0745
- val_mean_squared_error: 0.0097
Epoch 4/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.9989
- acc: 0.0889 - mean_squared_error: 0.0097 - val_loss: 3.9709 - val_acc: 0.0922
- val_mean_squared_error: 0.0096
Epoch 5/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.8207
- acc: 0.1175 - mean_squared_error: 0.0095 - val_loss: 3.8121 - val_acc: 0.1172
- val_mean_squared_error: 0.0095
Epoch 6/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.6638
- acc: 0.1444 - mean_squared_error: 0.0094 - val_loss: 3.6191 - val_acc: 0.1620
- val_mean_squared_error: 0.0093
Epoch 7/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.5202
- acc: 0.1695 - mean_squared_error: 0.0093 - val_loss: 3.5624 - val_acc: 0.1631
- val_mean_squared_error: 0.0093
Epoch 8/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.3970
- acc: 0.1940 - mean_squared_error: 0.0091 - val_loss: 3.5031 - val_acc: 0.1777
- val_mean_squared_error: 0.0092
Epoch 9/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.2684
- acc: 0.2160 - mean_squared_error: 0.0090 - val_loss: 3.3561 - val_acc: 0.2061
- val_mean_squared_error: 0.0090
Epoch 10/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.1532
- acc: 0.2383 - mean_squared_error: 0.0088 - val_loss: 3.2669 - val_acc: 0.2183
- val_mean_squared_error: 0.0089
让我们使用(当然是使用 matplotlib 库)图形化地查看训练和测试结果的指标。
plt.figure(0)
plt.plot(scnn.history['acc'],'r')
plt.plot(scnn.history['val_acc'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Accuracy")
plt.title("Training Accuracy vs Validation Accuracy")
plt.legend(['train','validation'])
plt.figure(1)
plt.plot(scnn.history['loss'],'r')
plt.plot(scnn.history['val_loss'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Loss")
plt.title("Training Loss vs Validation Loss")
plt.legend(['train','validation'])
plt.show()

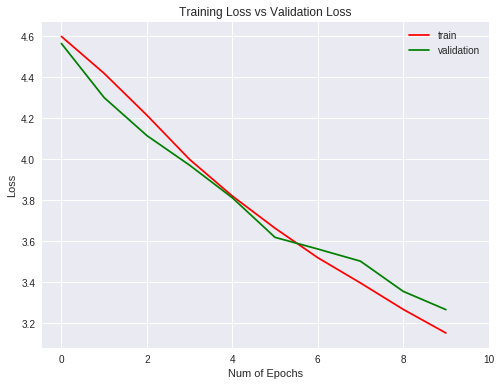
在这种情况下,泛化能力比常规网络要好,因为与简单网络的 4% 相比,它只有 2%,这也不是一个好结果。
混淆矩阵
训练完模型后,我们想在得出模型可用性结论之前查看其他指标。为此,我们将创建混淆矩阵,并从中查看 **精确率**、**召回率** 和 **F1 分数** 指标(请参阅维基百科)。
要创建混淆矩阵,我们需要对测试集进行预测,然后,我们可以创建混淆矩阵并显示这些指标。
scnn_pred = scnn_model.predict(x_test, batch_size=32, verbose=1)
scnn_predicted = np.argmax(scnn_pred, axis=1)
正如我们在上一章中所做的那样,预测数组中的每个较高值将是实际预测。实际上,通常的做法是采用一个偏置值来区分预测值是否可能为正。
Scikit Learn 库具有创建混淆矩阵的方法。
#Creamos la matriz de confusión
scnn_cm = confusion_matrix(np.argmax(y_test, axis=1), scnn_predicted)
# Visualiamos la matriz de confusión
scnn_df_cm = pd.DataFrame(scnn_cm, range(100), range(100))
plt.figure(figsize = (20,14))
sn.set(font_scale=1.4) #for label size
sn.heatmap(scnn_df_cm, annot=True, annot_kws={"size": 12}) # font size
plt.show()

下一步,显示指标。
scnn_report = classification_report(np.argmax(y_test, axis=1), scnn_predicted)
print(scnn_report)
precision recall f1-score support
0 0.40 0.49 0.44 100
1 0.36 0.20 0.26 100
2 0.19 0.24 0.21 100
3 0.12 0.07 0.09 100
4 0.11 0.01 0.02 100
5 0.12 0.13 0.12 100
6 0.25 0.19 0.22 100
7 0.28 0.17 0.21 100
8 0.18 0.24 0.20 100
9 0.25 0.35 0.29 100
10 0.00 0.00 0.00 100
11 0.13 0.15 0.14 100
12 0.24 0.24 0.24 100
13 0.24 0.15 0.18 100
14 0.18 0.03 0.05 100
15 0.12 0.20 0.15 100
16 0.29 0.21 0.24 100
17 0.23 0.57 0.33 100
18 0.20 0.31 0.25 100
19 0.11 0.05 0.07 100
20 0.41 0.40 0.41 100
21 0.30 0.24 0.27 100
22 0.16 0.13 0.14 100
23 0.37 0.38 0.37 100
24 0.31 0.49 0.38 100
25 0.16 0.11 0.13 100
26 0.18 0.09 0.12 100
27 0.14 0.20 0.17 100
28 0.22 0.24 0.23 100
29 0.20 0.26 0.22 100
30 0.35 0.19 0.25 100
31 0.09 0.04 0.06 100
32 0.24 0.19 0.21 100
33 0.24 0.16 0.19 100
34 0.20 0.15 0.17 100
35 0.12 0.14 0.13 100
36 0.16 0.37 0.22 100
37 0.13 0.14 0.14 100
38 0.05 0.04 0.04 100
39 0.19 0.10 0.13 100
40 0.12 0.11 0.11 100
41 0.35 0.55 0.43 100
42 0.10 0.14 0.12 100
43 0.18 0.25 0.21 100
44 0.17 0.07 0.10 100
45 0.50 0.03 0.06 100
46 0.18 0.12 0.14 100
47 0.32 0.40 0.35 100
48 0.38 0.35 0.36 100
49 0.26 0.18 0.21 100
50 0.05 0.05 0.05 100
51 0.16 0.14 0.15 100
52 0.65 0.40 0.49 100
53 0.31 0.56 0.40 100
54 0.28 0.31 0.29 100
55 0.08 0.01 0.02 100
56 0.30 0.28 0.29 100
57 0.16 0.33 0.22 100
58 0.27 0.13 0.17 100
59 0.15 0.18 0.17 100
60 0.61 0.68 0.64 100
61 0.11 0.43 0.18 100
62 0.49 0.21 0.29 100
63 0.16 0.22 0.19 100
64 0.11 0.22 0.15 100
65 0.04 0.02 0.03 100
66 0.05 0.05 0.05 100
67 0.22 0.17 0.19 100
68 0.48 0.46 0.47 100
69 0.29 0.36 0.32 100
70 0.26 0.34 0.29 100
71 0.50 0.47 0.48 100
72 0.19 0.03 0.05 100
73 0.38 0.29 0.33 100
74 0.13 0.14 0.13 100
75 0.37 0.24 0.29 100
76 0.36 0.50 0.42 100
77 0.12 0.13 0.12 100
78 0.10 0.06 0.08 100
79 0.10 0.16 0.12 100
80 0.03 0.03 0.03 100
81 0.29 0.13 0.18 100
82 0.62 0.59 0.61 100
83 0.22 0.20 0.21 100
84 0.06 0.06 0.06 100
85 0.22 0.23 0.23 100
86 0.20 0.35 0.25 100
87 0.12 0.11 0.12 100
88 0.13 0.23 0.17 100
89 0.18 0.30 0.22 100
90 0.13 0.03 0.05 100
91 0.41 0.35 0.38 100
92 0.16 0.10 0.12 100
93 0.19 0.09 0.12 100
94 0.27 0.58 0.37 100
95 0.38 0.27 0.31 100
96 0.17 0.18 0.17 100
97 0.18 0.19 0.19 100
98 0.07 0.04 0.05 100
99 0.12 0.06 0.08 100
avg / total 0.22 0.22 0.21 10000
嗯,与上一个相比没有太大区别。让我们看看 ROC 曲线。
ROC 曲线
ROC 曲线由二分类器使用,因为它是一个查看真阳性率与假阳性率的好工具。接下来的几行代码显示了多类分类 ROC 曲线的代码。此代码来自DloLogy,但您可以转到Scikit Learn 文档页面。
from sklearn.datasets import make_classification
from sklearn.preprocessing import label_binarize
from scipy import interp
from itertools import cycle
n_classes = 100
from sklearn.metrics import roc_curve, auc
# Plot linewidth.
lw = 2
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], scnn_pred[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), scnn_pred.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# Compute macro-average ROC curve and ROC area
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
plt.figure(1)
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes-97), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
# Zoom in view of the upper left corner.
plt.figure(2)
plt.xlim(0, 0.2)
plt.ylim(0.8, 1)
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(3), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()


不错。让我们看看一些预测结果。
imgplot = plt.imshow(x_train_original[0])
plt.show()
print('class for image 1: ' + str(np.argmax(y_test[0])))
print('predicted: ' + str(scnn_predicted[0]))

class for image 1: 49
predicted: 85
另一个结果。
imgplot = plt.imshow(x_train_original[3])
plt.show()
print('class for image 3: ' + str(np.argmax(y_test[3])))
print('predicted: ' + str(scnn_predicted[3]))

class for image 3: 51
predicted: 51
然后,我们将保存训练历史结果以供将来比较。
#Histórico
with open(path_base + '/scnn_history.txt', 'wb') as file_pi:
pickle.dump(scnn.history, file_pi)
指标比较
下一步是将上一次实验的指标与本次结果进行比较。我们将比较两个模型(卷积神经网络和常规网络)的 **准确率**、**损失** 和 **均方误差**。为此,我们需要加载在前面章节中保存的历史结果。
with open(path_base + '/simplenn_history.txt', 'rb') as f:
snn_history = pickle.load(f)
现在,我们已将之前的 snn_history 变量中的结果加载进来,然后进行图形化比较。
plt.figure(0)
plt.plot(snn_history['val_acc'],'r')
plt.plot(scnn.history['val_acc'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Accuracy")
plt.title("Simple NN Accuracy vs simple CNN Accuracy")
plt.legend(['simple NN','CNN'])

plt.figure(0)
plt.plot(snn_history['val_loss'],'r')
plt.plot(scnn.history['val_loss'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Loss")
plt.title("Simple NN Loss vs simple CNN Loss")
plt.legend(['simple NN','CNN'])

plt.figure(0)
plt.plot(snn_history['val_mean_squared_error'],'r')
plt.plot(scnn.history['val_mean_squared_error'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Mean Squared Error")
plt.title("Simple NN MSE vs simple CNN MSE")
plt.legend(['simple NN','CNN'])

最终结论
与之前的模型不同,这些线条没有趋于水平(曲线的斜率继续保持一个接近零的值),因此可以假定继续增加 epoch 数量以改进训练是有益的。卷积网络提高了整体准确率,并且比常规神经网络泛化得更好一些。
值得关注的点(但不要被欺骗……)
正如并非所有闪闪发光的东西都是黄金,我们对模型进行了(在已经训练好的基础上)额外 20 个 epoch 的训练。如果我们看到训练结果,将会看到以下内容:
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 58s 1ms/step - loss: 3.0416
- acc: 0.2552 - mean_squared_error: 0.0086 - val_loss: 3.2335 - val_acc: 0.2305
- val_mean_squared_error: 0.0089
Epoch 2/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.9324
- acc: 0.2783 - mean_squared_error: 0.0085 - val_loss: 3.1399 - val_acc: 0.2471
- val_mean_squared_error: 0.0087
Epoch 3/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.8245
- acc: 0.3031 - mean_squared_error: 0.0083 - val_loss: 3.1052 - val_acc: 0.2639
- val_mean_squared_error: 0.0086
Epoch 4/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.7177
- acc: 0.3186 - mean_squared_error: 0.0081 - val_loss: 3.0722 - val_acc: 0.2696 - val_mean_squared_error: 0.0086
Epoch 5/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.6060
- acc: 0.3416 - mean_squared_error: 0.0079 - val_loss: 2.9785 - val_acc: 0.2771 - val_mean_squared_error: 0.0084
Epoch 6/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.4995
- acc: 0.3613 - mean_squared_error: 0.0077 - val_loss: 3.0285 - val_acc: 0.2828 - val_mean_squared_error: 0.0085
Epoch 7/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.3825
- acc: 0.3873 - mean_squared_error: 0.0075 - val_loss: 3.0384 - val_acc: 0.2852 - val_mean_squared_error: 0.0085
Epoch 8/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.2569
- acc: 0.4119 - mean_squared_error: 0.0073 - val_loss: 3.1255 - val_acc: 0.2804 - val_mean_squared_error: 0.0086
Epoch 9/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.1328
- acc: 0.4352 - mean_squared_error: 0.0070 - val_loss: 3.0136 - val_acc: 0.2948 - val_mean_squared_error: 0.0084
Epoch 10/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.0036
- acc: 0.4689 - mean_squared_error: 0.0067 - val_loss: 3.0198 - val_acc: 0.2951 - val_mean_squared_error: 0.0085
Epoch 11/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.8671
- acc: 0.4922 - mean_squared_error: 0.0065 - val_loss: 3.1819 - val_acc: 0.2958 - val_mean_squared_error: 0.0086
Epoch 12/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.7304
- acc: 0.5227 - mean_squared_error: 0.0061 - val_loss: 3.2325 - val_acc: 0.3062 - val_mean_squared_error: 0.0087
Epoch 13/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.5885
- acc: 0.5527 - mean_squared_error: 0.0058 - val_loss: 3.2594 - val_acc: 0.3041
- val_mean_squared_error: 0.0087
Epoch 14/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.4592
- acc: 0.5861 - mean_squared_error: 0.0055 - val_loss: 3.3133 - val_acc: 0.2987
- val_mean_squared_error: 0.0088
Epoch 15/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.3199
- acc: 0.6170 - mean_squared_error: 0.0051 - val_loss: 3.5305 - val_acc: 0.3004
- val_mean_squared_error: 0.0090
Epoch 16/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.1907
- acc: 0.6491 - mean_squared_error: 0.0047 - val_loss: 3.6840 - val_acc: 0.3080
- val_mean_squared_error: 0.0091
Epoch 17/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.0791
- acc: 0.6787 - mean_squared_error: 0.0044 - val_loss: 3.8013 - val_acc: 0.2965
- val_mean_squared_error: 0.0093
Epoch 18/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.9594
- acc: 0.7100 - mean_squared_error: 0.0040 - val_loss: 3.8901 - val_acc: 0.2967
- val_mean_squared_error: 0.0094
Epoch 19/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.8585
- acc: 0.7362 - mean_squared_error: 0.0036 - val_loss: 4.0126 - val_acc: 0.2957
- val_mean_squared_error: 0.0095
Epoch 20/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.7647
- acc: 0.7643 - mean_squared_error: 0.0033 - val_loss: 4.3311 - val_acc: 0.2954
- val_mean_squared_error: 0.0099


发生了什么?
如果成功率相对于前 10 个 epoch 有所提高,那么随着训练次数的增加,它开始泛化得更少。可以看出,验证数据的损失函数在达到 3 的值时达到最小值,然后开始增加。在准确率图上,它表明算法的改进不超过 30%。从这里开始,可以选择使用正则化方法或更换更好的模型。
在下一篇文章中,我们将介绍 ResNET。下次再见!
历史
- 2018 年 5 月 31 日:初版
