探索计算数论（第 3 部分）

C#

• 下载源代码 - 47.3 KB
• 下载 BigIntegerExcelDNA.zip - 2.3 MB
• 下载 ExcelDna-0.32.zip - 1.4 MB

VBA

• 下载 ProgramsVBA.zip - 67.1 KB

Excel

• 下载 Excel.zip - 9.4 MB

单词

• 下载 Word.zip - 3.6 MB

引言

在《探索计算数论（第一部分）》中，我们描述了一种确定任意正整数指数的欧拉素数/伪素数的方法。在《半素数有序序列（第二部分）》中，我们描述了一种在无限域上对半素数二元序列进行排序的方法。

本文介绍了一种分解经典整数的方法。与《探索计算数论（第一部分）》一样，本文引用其他作者的资料以获得支持，具体如下：

1. Mihnea Rădulescu 的《"BigInteger Library"》，发布于 2011 年 9 月 23 日，地址：https://codeproject.org.cn/Articles/60108/BigInteger-Library
2. Chew Keong TAN 的《"C# BigInteger Class"》，发布于 2002 年 9 月 28 日，地址：https://codeproject.org.cn/Articles/2728/C-BigInteger-Class
3. Adam Tibi 的《"Using C# .NET User Defined Functions (UDF) in Excel"》，发布于 2013 年 6 月 13 日，地址：https://codeproject.org.cn/Articles/606446/UsingplusC-plus-NETplusUserplusDefinedplusFuncti
4. Excel-DNA 版本 0.32 可在此处获取：http://exceldna.codeplex.com/releases/view/119190。
5. Thomas Maierhofer (Tom) 的《"Performance Tests: Precise Run Time Measurements with System.Diagnostics.Stopwatch"》，发布于 2010 年 2 月 28 日，地址：https://codeproject.org.cn/Articles/61964/Performance-Tests-Precise-Run-Time-Measurements-wi

背景

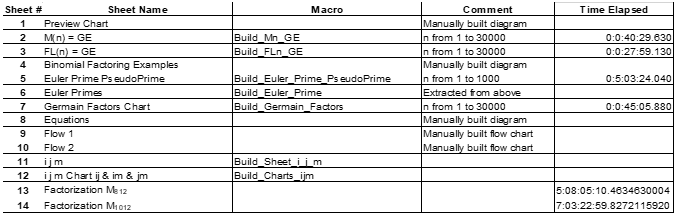
在《探索计算数论（第三部分）》中，我们将扩展一种分解梅森数 2ⁿ – 1、费马-卢卡斯数 2ⁿ + 1 和欧拉数的方法，这些方法在《探索计算数论（第一部分）》中已有所介绍。下面的图表 1 展示了用于生成本文每个分解步骤中使用的表格所需的时间资源，同时也作为本文的目录。这些时间是在一台运行其他应用程序的笔记本电脑上生成的，而不是在实时或优化基准系统上。这仅是一个一般性的时间参考，如果您决定重新生成表格，预期的时间可能会有很大的差异。

下面的图表 1 概述了经典整数的层级结构及其相互关系以及将要探讨的分解过程。

梅森数

通过确定 n 的因子组合，梅森数可以重写为欧拉数的因子。图表 2 是一个将梅森数重写为欧拉数的示例。

本项目提供的 C# 代码包含一种方法，可以从 n 的因子中确定因子组合。以下 C# 代码通过这些组合生成梅森数的欧拉因子。

if ((long)combin[0, 0] > 1)
    for (index = 0; index <= fac.GetUpperBound(0); index++)
    {
        ord = Order(fac[index, 0].ToString(), 2);
        for (jndex = 0; jndex <= combin.GetUpperBound(0); jndex++)
            if ((long)combin[jndex, 0] == ord)
                if (Euler((long)combin[jndex, 0]) / Convert.ToInt64(fac[index, 0]) == 1)
combin[jndex, 1] = Convert.ToInt64(combin[jndex, 1]) +         Convert.ToInt64(fac[index, 1]);
    }
return combin;

费马-卢卡斯数

与梅森数类似，通过确定 n 的因子组合，费马-卢卡斯数也可以重写为欧拉数的因子。下面的图表 3 是一个示例。

以下 C# 代码通过 n 的因子组合生成费马-卢卡斯数的欧拉因子。

while (testValue % 2 == 0)
{
    testValue /= 2;
    twoExp++;
}
testValue = (long)Math.Pow(2, twoExp);

for (index = 0; index <= MerE.GetUpperBound(0); index++)
{
    if ((long)MerE[index, 0] % testValue == 0)
    {
        if (Temp == null || Temp.Length == 0)
            Temp = new object[1, 2];
        else
        {
            // Redimension Temp
            Hold = new object[Temp.GetLength(0), Temp.GetLength(1)];
            for (jndex = 0; jndex <= Temp.GetUpperBound(0); jndex++)
                for (kndex = 0; kndex <= Temp.GetUpperBound(1); kndex++)
                    Hold[jndex, kndex] = Temp[jndex, kndex];
            Temp = new object[Hold.GetLength(0) + 1, Hold.GetLength(1)];
            for (jndex = 0; jndex <= Hold.GetUpperBound(0); jndex++)
                for (kndex = 0; kndex <= Hold.GetUpperBound(1); kndex++)
                    Temp[jndex, kndex] = Hold[jndex, kndex];
        }
        Temp[Temp.GetUpperBound(0), 0] = MerE[index, 0];
        Temp[Temp.GetUpperBound(0), 1] = MerE[index, 1];
    }
}
return Temp;

下面的图表 2 和 3 是梅森数二项分解的两个示例。虽然这种方法对于分解不是必需的，但在将梅森数和费马-卢卡斯数重写为欧拉数后，这里包含它们是为了理解和完整性。

欧拉

在“第一部分”中，我们推导并定义了欧拉数为 E_n = 1 mod n，即 E_n = c * n + 1，其中 c 是正整数，n 是以 2 为底的最小正指数。下面的图表 4 显示了 n <= 1000 的欧拉素数。我们使用 Miller-Rabin 概率测试来确定素性。此外，在图表 4 中，E₁ = 1 和 E₆ = 1 被标记为“FALSE”。

热尔曼数

在第一部分中，热尔曼数被定义为 G_n = c*n+1，其中 c 是正整数，n 是以 2 为底的最小正指数。如果 n 为奇数或 n = 2^x，则 G_n = 2k*n+1 或 c = 2k。如果 n 为偶数（n = 2^x 除外），则 G_n = c * n + 1。在上面的二项分解示例中，每个示例都有一个必须考虑的热尔曼因子。下面的图表 1 显示了这些因子的分布。

下面的 C# 代码生成梅森数和费马-卢卡斯数的热尔曼因子。

if (odd)
    M_FL_E = Mersenne2Euler(number);
else
    M_FL_E = FermatLucas2Euler(number);

for (index = 0; index <= fac.GetUpperBound(0); index++)
{
    ord = Order(fac[index, 0].ToString(), 2);
    if (ord % 2 == 0 || odd)
        for (jndex = 0; jndex <= M_FL_E.GetUpperBound(0); jndex++)
            if ((long)M_FL_E[jndex, 0] == ord)
            {
                if (Euler((long)M_FL_E[jndex, 0]) / (BigInteger)(fac[index, 0].ToString()) > 1)
                    if (Temp == null || Temp.Length == 0)
                        Temp = new object[1, 3];
                    else
                    {
                        // Redimension Temp
                        Hold = new object[Temp.GetLength(0), Temp.GetLength(1)];
                        for (kndex = 0; kndex <= Temp.GetUpperBound(0); kndex++)
                            for (lndex = 0; lndex <= Temp.GetUpperBound(1); lndex++)
                                Hold[kndex, lndex] = Temp[kndex, lndex];
                        Temp = new object[Hold.GetLength(0) + 1, Hold.GetLength(1)];
                        for (kndex = 0; kndex <= Hold.GetUpperBound(0); kndex++)
                            for (lndex = 0; lndex <= Hold.GetUpperBound(1); lndex++)
                                Temp[kndex, lndex] = Hold[kndex, lndex];
                    }
                    Temp[Temp.GetUpperBound(0), 0] = fac[index, 0];
                    Temp[Temp.GetUpperBound(0), 1] = fac[index, 1];
                    Temp[Temp.GetUpperBound(0), 2] = M_FL_E[jndex, 0];
            }
}
return Temp;

欧拉-热尔曼分解

以下方程构成了欧拉-热尔曼分解的基础。有关二次方程和勾股定理集成的信息和方法，请参阅《选定的 RSA 数的分解算法》。

从上面的流程 1 和 2 中，可以构建一个二次方程列表，如下面的图表 5 所示。

图表 2	图表 3
图表 4	图表 5
图表 6	图表 7

上面的图表 2 显示了流程 1 搜索算法的线性性质，而上面的图表 3 显示了流程 2 的非线性性质。由于流程 2 算法的资源密集型特性，可以排除流程 2 而依赖流程 1。但是，如果 i 和 j 的大小非常接近（参见图表 3），并且解决方案存在于非线性范围内，性能将会下降。如果将 i、j 和 m 集成到一个低资源非线性公式中，可以实现更快的性能。在第一部分中，我们提到“从大的欧拉数中找到热尔曼伪素数仍然非常耗时，并且与欧拉数不同，目前似乎没有办法直接计算热尔曼数”。这是由于一个悬而未决的问题：“是否存在一个公式能够等同于在 min i 到 max i 的范围内，当 order_{in + 1}2 = n 时？”因为所有正整数解都必须在此范围内并具有此形式。如果在此范围内没有整数解，则正在评估的整数是素数或单位。下面的 C# 代码片段使用流程 1 逻辑在一个紧密循环中搜索解。还可以采用进一步的调整来减少计算时间。例如，如果 n 为奇数，则 i 和 j 都为偶数；因此，k – i 必须为偶数，因为偶数 / 奇数 = 偶数。

long inc;
inc = 1;
if (i == 0)
    i = 1;
if (BigInteger.IsBitSet(n, 0))
{
     inc = 2;
     if (BigInteger.IsBitSet(i, 0))
         i++;
}
time = Stopwatch.StartNew();
BigInteger k = (E - 1) / n;
BigInteger h = BigInteger.IntegerSqrt(k);
while (k % (i * n + 1) != i && time.ElapsedMilliseconds < t && i <= h)
    i += inc;
time.Stop();

图表 6 和 7 是使用上面的 C# 代码在图表 2 和 3 中对 M₈₁₂ 和 M₁₀₁₂ 的分解。

Using the Code

本项目是一个概念原型，因此不像更成熟的产品那样具备用户友好的错误检查功能。C# 代码自第一部分以来只做了极少量的修改，因此与原始版本非常接近。Excel-DNA 软件已配置为支持 32 位或 64 位系统。BigInterger Library 已修改并扩展以支持本项目。代码应可用于 C# 项目、Excel VBA 和 Excel 电子表格中的实验。要在 Excel 中使用，请在电子表格中打开 BigInteger-packed.xll，将有两个函数库：“BigInteger”和“Number Theory”。在 VBA 环境中引用 BigInteger-packed.xll 是某些宏构建本项目使用的电子表格或在其他 VBA 应用程序中使用所必需的。Microsoft Excel 需要引用以下库：

1. Visual Basic For Applications
2. Microsoft Excel 16.0 Object Library
3. OLE Automation
4. Microsoft Office 16.0 Object Library
5. BigIntExcel

如果您使用的是 .NET 4.0 或更高版本，您可能希望修改此项目代码以使用 Microsoft 的 Numeric 库。根据我的研究，除法算法是准确性和速度的关键。

关注点

由于“RegisterSize”函数会更改静态字段的值，因此此代码不是线程安全的。通过删除此函数，可以相对直接地使本项目成为线程安全的。目前，我尚未探索在多 CPU 环境中使用并行处理。Microsoft Excel 2007 或 Excel 2016 中 BigInteger 的最大大小为 32,767 位十进制数字，如果超过此阈值，将会导致计算错误。请参阅https://support.office.com/en-us/article/excel-specifications-and-limits-1672b34d-7043-467e-8e27-269d656771c3?ui=en-US&rs=en-001&ad=US#ID0EBABAAA=2016,_2013。查找大数 BigInteger 阶的算法在查找大 e 的整数阶时速度很慢。*D:\BaseASeq\ProgramsC#\ExcelDna-0.32\Distribution\ExcelDnaPack.noexe 应在编译 C# 代码之前更改为 .exe。我已经删除了 ExcelDNA 中的所有 .exe 文件，因此如果需要，需要重新编译或从原始 zip 文件中解压缩。

历史

这是该软件的第二个版本。